ТОМА ПРОСТРАНСТВО

- топологич. пространство, сопоставляемое векторному (или сферическому) расслоению.
Пусть . векторное расслоение над клеточным пространством X. Пусть в нем выбрана риманова метрика и рассматривается ассоциированное с расслоение 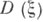на замкнутые единичные диски. В содержится подрасслоение 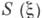на единичные сферы; факторпространство есть пространство Тома расслоения обозначаемое Для компактной базы XТ. п. можно описать также как одноточечную компактификацию тотального пространства расслоения Кроме того, Т. п. является конусом проекции 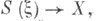и можно таким образом определять Т. п. любого сферич. расслоения. Конечно, Т. п. определены и для любых расслоений со слоем
Пусть О _k - группа ортогональных преобразований пространства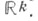 Над ее классифицирующим пространством BO_k имеется k-мерное векторное расслоение ассоциированное с универсальным О _k -расслоением. Т. п. часто обозначается через МО _k или ТВО _k и наз. пространством Тома группы O_k. Аналогично вводятся Т. п. MU_k, 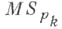и т. д., где U_k и 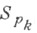соответственно - унитарная и симплектическая группы.
Роль Т. п. состоит в том, что они позволяют сводить ряд геометрич. задач к задачам гомотопич. топологии и, следовательно, к алгебраич. задачам. Так, задача вычисления групп бордизмов сводится к задаче вычисления гомотопич. групп Т. п. МО _k, MSO_k и т. д. (см. [1], [2], а также Кобордизм);задача классификации гладких многообразий сводится к исследованию гомотопич. свойств Т. п. нормального расслоения (см. [3]); задача реализации циклов подмногообразиями (см. Стинрода задача )сводится к изучению когомологий Т. п. MSO_k и МО _k, и т. д. (см. также Трансвереальное отображение, Трубчатая окрестность).
Конструкция Т. н. естественна на категории расслоений: любой морфизм (векторных) расслоений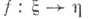 индуцирует непрерывное отображение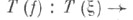 В частности, Т. п. n-мерного расслоения над точкой есть Sⁿ, и потому для любого n-мерного векторного расслоения над Xи любой точкой имеется включение (индуцированное включением слоя над х).Если Xлинейно связно, то все такие включения гомотопны, и можно говорить об отображении единственном с точностью до гомотопности.
Для векторных расслоений и над Xи Yсоответственно определено расслоение над При этом (см. [4]). В частности, для тривиального расслоения имеет место где S - оператор надстройки, так что Это обстоятельство позволяет конструировать всевозможные спектры пространств Тома.
Для мультипликативной обобщенной теории когомологий Е имеется спаривание

Возникает спаривание

так что является Е* (Х) -модулем, и это используется при построении Тома изоморфизма.
Важной и часто используемой является следующая теорема двойственности Атьи (см. [4], [5]): если М - гладкое многообразие с краем дМ (возможно пустым) и v - его нормальное расслоение, то Т. п. Т(v) находится в S-двойственности к М/дМ.

Лит.:[1] Тoм Р., в кн.: Расслоенные пространства и их приложения. Сб. пер., М., 1958, с. 293-351; [2] Стонг Р., Заметки по теории кобордизмов, пер. с англ., М., 1973; [3] Браудер В., Перестройки односвязных многообразий, пер. с англ., М., 1983; [4] Xьюзмоллер Д., Расслоенные пространства, пер. с англ., М., 1970; [5] Атья М., лМатематика