СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ

СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ

построение обобщенных сумм расходящихся рядов с помощью суммирования методов. Если по нек-рому правилу Рряду


относят число s, называемое его суммой ряда, то говорят, что ряд суммируем к сумме s методом суммирования Рили Р-суммируем к сумме s и этот факт обозначается одним из символов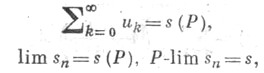

где sn - частичные суммы ряда (*). Числом в этом случае наз. также Р-суммой ряда. Напр., для ряда (*) рассматривают последовательность 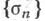средних арифметических первых nчастичных сумм ряда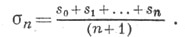


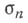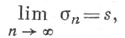Если при этом имеет предел при 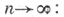то говорят, что ряд (*) суммируем к сумме s средних арифметических методом суммирования и обозначают символом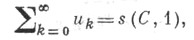


или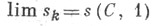


(см. Чезаро методы суммирования).
При таком определении суммы ряда каждый сходящийся ряд суммируем, причем к той же сумме, к к-рой он сходится, и, кроме того, существуют расходящиеся ряды, суммируемые этим методом. Напр., ряд 1 -1+1-1 + ... суммируем указанным методом и его ( С,1)-сумма равна 1/2.
Определение метода суммирования обычно подчиняется ряду требований. Напр., требуют, чтобы метод суммировал целый класс рядов; чтобы не противоречил сходимости, т. е., будучи применен к сходящемуся ряду, суммировал бы его к той же сумме, к к-рой ряд сходится (см. Регулярные методы суммирования);чтобы из суммируемости рядов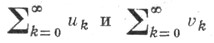


данным методом соответственно к суммам ии vследовала суммируемость ряда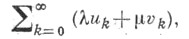


причем к сумме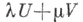 (свойство линейности). См. также Расходящийся ряд.

Лит.:[1] Харди Г., Расходящиеся ряды, пер. с англ., М-., 1951; [2] Кук Р., Бесконечные матрицы и пространства последовательностей, пер. с англ., М., 1960; [3] Кангро Г. Ф., в сб.: Итоги науки и техники. Математический анализ, т. 12, М., 1974, с. 5-70; [4] Барон С., Введение н теорию суммируемости рядов, Таллин, 1977; [5] Реуегimhоff A., Lectures on summability, В., 1969; [6] Кnорр К., Theory and application on infinite series, N. Y., 1971; [7] Ze11er K., Beekmann V., Theorie der Limitierungsverfahren, 2 Aufl., B,-Hdlb.-N. Y., 1970; [8] Petersen G. M., Regular matrix transformations, L., 1966.
И. И. Волков.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужен реферат?

Полезное


Смотреть что такое "СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ" в других словарях:

  • Суммирование —         расходящихся рядов и интегралов, построение обобщённой суммы Ряда (соответственно значения Интеграла), не имеющего обычной суммы (соответственно значения). Расходящиеся ряды могут получаться при перемножении условно сходящихся рядов, при… …   Большая советская энциклопедия

  • Сходимость —         математическое понятие, означающее, что некоторая переменная величина имеет Предел. В этом смысле говорят о С. последовательности, С. ряда, С. бесконечного произведения, С. непрерывной дроби, С. интеграла и т. д. Понятие С. возникает,… …   Большая советская энциклопедия

  • РАСХОДЯЩИЙСЯ РЯД — ряд, у к рого последовательность частичных сумм не имеет конечного предела. Напр., ряды расходятся. Р. р. стали появляться в работах математиков 17 18 вв. Л. Эйлер (L. Euler) первым пришел к выводу, что нужно ставить вопрос, не чему равна сумма,… …   Математическая энциклопедия

  • Расходящиеся интегралы —         интегралы с бесконечными пределами, а также с неограниченной подынтегральной функцией, равные бесконечности или же не имеющие определённого конечного значения. Например, интеграл Несобственные интегралы, Интеграл, Суммирование… …   Большая советская энциклопедия

  • Расходящийся ряд —         ряд, у которого последовательность частичных сумм не имеет конечного предела. Если общий член ряда не стремится к нулю, то ряд расходится, например 1 1 + 1 1 + ... + ( 1) n 1 + ...; примером Р. p., общий член которого стремится к нулю,… …   Большая советская энциклопедия

  • Тауберовы теоремы —         теоремы, устанавливающие условия, при которых суммируемость ряда или интеграла некоторым методом влечёт его суммируемость более слабым методом (см. Суммирование расходящихся рядов и интегралов). Одной из первых теорем такого типа была… …   Большая советская энциклопедия

  • 1 − 2 + 3 − 4 + … — Первые 15000 частичных сумм ряда 0 + 1 − 2 + 3 − 4 + … В математике, 1 − 2 + 3 − 4 + … это числовой ряд, слагаемые которого по модулю представляют собой последовательные натуральные …   Википедия

  • РЯДЫ — Многие задачи в математике приводят к формулам, содержащим бесконечные суммы, например, или Такие суммы называются бесконечными рядами, а их слагаемые членами ряда. (Многоточие означает, что число слагаемых бесконечно.) Решения сложных… …   Энциклопедия Кольера

  • ЭПСИЛОН-РАЗЛОЖЕНИЕ — (e разложение) метод приближённого вычисления критических показателей в ста тистич. физике [или аномальных размерностей в квантовой теории поля (КТП)] с помощью разложения корреляц. ф ций и др. физ. величин вблизи критической точки… …   Физическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»