- СПИНОРНАЯ СТРУКТУРА
на т-мерном многообразии М, расслоение спин-реперов, - главное расслоение
 над Мсо структурной группой Spin (n)(см. Спинорная группа). накрывающее нек-рое главное расслоение
над Мсо структурной группой Spin (n)(см. Спинорная группа). накрывающее нек-рое главное расслоение  кореперов со структурной группой SO (n). Последнее условие означает, что задан тождественный по базе сюръективныи гомоморфизм
кореперов со структурной группой SO (n). Последнее условие означает, что задан тождественный по базе сюръективныи гомоморфизм  главных расслоении
главных расслоении  согласованный с естественным гомоморфизмом
согласованный с естественным гомоморфизмом 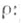
 Говорят, что С. с.
Говорят, что С. с. 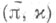 подчинена рцмановой метрике g на М, определяемой расслоением
подчинена рцмановой метрике g на М, определяемой расслоением 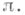 С точки зрения теории G-структур С. с. есть обобщенная G-структура со структурной группой G=Spin(n), рассматриваемой вместе с неточным представлением
С точки зрения теории G-структур С. с. есть обобщенная G-структура со структурной группой G=Spin(n), рассматриваемой вместе с неточным представлением 

Аналогичным образом определяются С. с., подчиненная псевдоримановой метрике, и С. с. на комплексном многообразии, подчиненная комплексной метрике. Необходимые н достаточные условия существования С. с. на Мсостоят в ориентируемости многообразия Ми обращении в нуль класса Штифеля - Уитни W2(M). При выполнении этих условий число неизоморфных С. с. на M, подчиненных данной римановой метрике, совпадает с порядком группы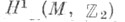 (см. [6]). Пусть С - комплексификация Клиффорда алгебры пространства
(см. [6]). Пусть С - комплексификация Клиффорда алгебры пространства  относительно квадратичной формы
относительно квадратичной формы  Алгебра Собладает неприводимым представлением в пространстве . над
Алгебра Собладает неприводимым представлением в пространстве . над 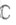 размерности
размерности 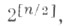 к-рое определяет представление группы Spin
к-рое определяет представление группы Spin в пространстве S. Всякая С. с.
в пространстве S. Всякая С. с. 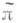 на Мзадает ассоциированное векторное расслоение
на Мзадает ассоциированное векторное расслоение  со слоем S, называемое расслоением спиноров. Риманова связность на Мопределяет каноничегким образом связность в расслоении
со слоем S, называемое расслоением спиноров. Риманова связность на Мопределяет каноничегким образом связность в расслоении  В пространстве Г (S)гладких сечений расслоения
В пространстве Г (S)гладких сечений расслоения  (спинорных полей) действует линейный дифференциальный оператор Dпорядка 1 - оператор Дирака, к-рый локально определяется формулой
(спинорных полей) действует линейный дифференциальный оператор Dпорядка 1 - оператор Дирака, к-рый локально определяется формулой 
где
 - ковариантные производные по направлениям ортонормированных векторных полей si, а умножение элементов из Sна векторы из
- ковариантные производные по направлениям ортонормированных векторных полей si, а умножение элементов из Sна векторы из  соответствует определенной выше структуре С-модуля на S.
соответствует определенной выше структуре С-модуля на S.
Спинорные поля, аннулируемые оператором D, иногда наз. гармоническими. Если Мкомпактно, то причем эта размерность не меняется при конформной деформации метрики [4]. Если при этом риманова метрика на Мимеет положительную скалярную кривизну, то kerD = 0 (см. [4], [5]).
причем эта размерность не меняется при конформной деформации метрики [4]. Если при этом риманова метрика на Мимеет положительную скалярную кривизну, то kerD = 0 (см. [4], [5]).
С. с. в пространстве-времени ( М, g) (т. е. в четырехмерном лоренцевом многообразии) наз. С. с., подчиненная лоренцевой метрике g. Существование С. с. в некомпактном пространстве-времени . эквивалентно абсолютной параллелизуемости многообразия М(см. [3]).Пространство спиноров Sкак модуль над спинорной группой Spin разлагается в прямую сумму двух комплексных двумерных комплексно-сопряженных SL (2, G)-модулой
разлагается в прямую сумму двух комплексных двумерных комплексно-сопряженных SL (2, G)-модулой 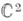 и
и  Этому разложению соответствует разложение
Этому разложению соответствует разложение  расслоения спиноров, причем тензорное произведение
расслоения спиноров, причем тензорное произведение  отождествляется с комплексификацией касательного расслоения ТМ. Спинорные поля в пространстве-времени, являющиеся собственными функциями оператора Дирака, описывают свободные поля частиц со спином 1/2 напр. электронов.
отождествляется с комплексификацией касательного расслоения ТМ. Спинорные поля в пространстве-времени, являющиеся собственными функциями оператора Дирака, описывают свободные поля частиц со спином 1/2 напр. электронов. Лит.:[1] Казанова Г., Векторная алгебра, пер. с франц., М., 1979; [2] Пенроуз Р., Структура пространства-времени, пер. с англ., М., 1972; [3] Gerосh R., лJ. Math. Phys.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
