- СОПРЯЖЕННЫЙ ТРИГОНОМЕТРИЧЕСКИЙ РЯД
- к ряду
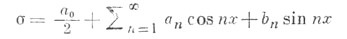
- ряд
Эти ряды являются соответственно действительной и мнимой частями ряда

при z=eix. Формула для частных сумм
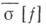 сопряженного к ряду Фурье функции j(x)тригонометрич. ряда
сопряженного к ряду Фурье функции j(x)тригонометрич. ряда 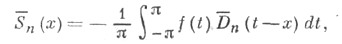
где
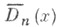 - сопряженное Дирихле ядро. Если f(x) -функция ограниченной вариации на
- сопряженное Дирихле ядро. Если f(x) -функция ограниченной вариации на 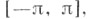 то необходимым и достаточным условием сходимости ряда
то необходимым и достаточным условием сходимости ряда 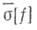 в точке х 0 является существование сопряженной функции (см. п. 3)
в точке х 0 является существование сопряженной функции (см. п. 3)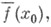 к-рая представляет тогда сумму ряда
к-рая представляет тогда сумму ряда 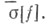 Если f(x) - суммируемая на
Если f(x) - суммируемая на 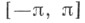 функция, то ряд
функция, то ряд  суммируется почти всюду методами
суммируется почти всюду методами  и методом Абеля - Пуассона и почти всюду совпадает с сопряженной функцией f(x). Если функция
и методом Абеля - Пуассона и почти всюду совпадает с сопряженной функцией f(x). Если функция 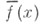 суммируема, то сопряженный ряд
суммируема, то сопряженный ряд 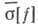 является ее рядом Фурье. Функция
является ее рядом Фурье. Функция 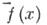 может быть несуммируемой; для таких обобщений интеграла Лебега, как А-интеграл и Бокса интеграл, сопряженный ряд
может быть несуммируемой; для таких обобщений интеграла Лебега, как А-интеграл и Бокса интеграл, сопряженный ряд 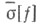 всегда является рядом Фурье сопряженной функции.
всегда является рядом Фурье сопряженной функции. Лит.:[1] Тauber A., лMonatsch. Math. Phys.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
