БИРАЦИОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ
- БИРАЦИОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ
бирациональное отображение алгебраич. многообразия (или схемы) в себя. Б. п. иногда наз. также бирациональными автоморфизмами. Группа всех Б. п. алгебраич. .многообразия канонически изоморфна группе автоморфизмов его поля рациональных функций над полем констант. Примерами Б. п. могут служить кремоновы преобразования, в частности стандартное квадратичное преобразование проективной плоскости, задаваемое формулой
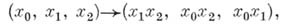
где 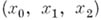 - однородные координаты проективной плоскости. И. В. Долгачее, В. А. Псковских.
- однородные координаты проективной плоскости. И. В. Долгачее, В. А. Псковских.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "БИРАЦИОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ" в других словарях:
Бирациональное преобразование — точечное преобразование плоскости, при котором любая точка Р преобразуется в точку Р так, что координаты точки P рационально выражаются через координаты точки Р и, наоборот, координаты точки Р рационально выражаются через координаты точки … Большая советская энциклопедия
Преобразование — одно из основных понятий математики, возникающее при изучении соответствий между классами геометрических объектов, классами функций и т.п. Например, при геометрических исследованиях часто приходится изменять все размеры фигур в одном и… … Большая советская энциклопедия
КРЕМОНОВО ПРЕОБРАЗОВАНИЕ — бирациональное преобразование проективного пространства над полем k. Бирациональные преобразования плоскости и трехмерного пространства систематически изучал (начиная с 1863) Л. Кремона (L. Cremona). Группа К. п также называется его именем группа … Математическая энциклопедия
БИРАЦИОНАЛЬНОЕ ОТОБРАЖЕНИЕ — бирациональный изоморфизм, рациональное отображение алгебраич. многообразий, индуцирующее изоморфизм их полей рациональных функций. В более общем смысле, рациональное отображение схем наз. бирациональным отображение м, если оно удовлетворяет… … Математическая энциклопедия
ГЕОМЕТРИИ ОБЗОР — Геометрия раздел математики, тесно связанный с понятием пространства; в зависимости от форм описания этого понятия возникают различные виды геометрии. Предполагается, что читатель, приступая к чтению этой статьи, обладает некоторыми… … Энциклопедия Кольера
Кремона — I Кремона (Cremona) Луиджи (7.12.1830, Павия, 10.6.1903, Рим), итальянский математик. С 1873 профессор и директор инженерной школы в Риме. Основные работы относятся к начертательной геометрии, графостатике и алгебраической геометрии. Им… … Большая советская энциклопедия
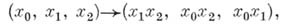
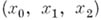 - однородные координаты проективной плоскости. И. В. Долгачее, В. А. Псковских.
- однородные координаты проективной плоскости. И. В. Долгачее, В. А. Псковских.