СЕРИЙ СХЕМА

последовательность серий,- двойная последовательность случайных величин , в к-рой случайные величины , образующие n-ю серию, взаимно независимы при любом п. Простейшая С. с. соответствует случаю k_n=n. Класс случайных величин, образующих С. с., играет в предельных теоремах теории вероятностей особую роль, к-рая определяется предельным поведением при распределений сумм случайных величин:

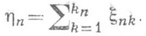(4)

При определенных условиях класс предельных распределений для таких последовательностей совпадает с классом безгранично делимых распределений. Именно, пусть С. с. 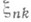удовлетворяет условию бесконечной малости (условию асимптотической пренебрегаемости), то есть при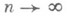

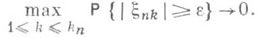(2)

Говорят, что 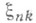образуют нулевую схему серий. Тогда множество распределений, предельных в смысле слабой сходимости для распределений (1), где - нулевая С. с., удовлетворяющая условию бесконечной малости, совпадает с множеством безгранично делимых распределений.

Известны условия сходимости распределений h_n к заданному безгранично делимому распределению (см. [1]). В частности, условие сходимости к нормальному распределению имеет следующий вид.

Пусть есть С. с., 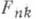- функция распределения 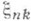. Для того чтобы 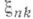удовлетворяла условию (2) и распределение сумм (1) слабо сходилось к нормальному распределению с параметрами a и b, необходимо и достаточно, чтобы для любого фиксированного e>0 выполнялись условия:

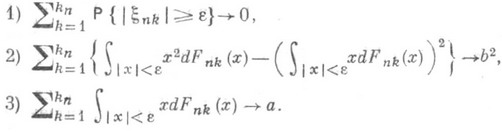
Изучение предельных распределений для нормированных частичных сумм последовательности независимых случайных величин сводится к С. с.

По поводу С. с. см. также Безгранично делимое распределение, Больших чисел закон, Предельные теоремы. Так, напр., в классич. вариантах центральной предельной теоремы и закона больших чисел рассматриваются частные случаи С. с., образованные случайными величинами

где 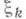- независимые случайные величины.

Лит.:[1] Г н е д е н к о Б. В., К о л м о г о р о в А. Н., Предельные распределения для сумм независимых случайных величин, М.-Л., 1949; [2] П р о х о р о в Ю. В., Р о з а н о в Ю. А., Теория вероятностей, 2 изд., М., 1973; [3] II е т р о в В. В., Суммы независимых случайных величин, М., 1972; [4] Ф е л л е р В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 2, М., 1967. Н. Г. Ушаков.