Регулярное пространство — Определению топологического пространства удовлетворяет очень широкий класс множеств. В частности, оно включает пространства, топология которых мало похожа на топологию метрического пространства. Поэтому, на топологические пространства часто… … Википедия
Вполне регулярное пространство — или тихоновское пространство топологическое пространство, удовлетворяющее аксиоме отделимости T3½, то есть такое топологическое пространство, в котором для любого замкнутого множества и точки вне его существует непрерывная числовая функция … Википедия
ВПОЛНЕ РЕГУЛЯРНОЕ ПРОСТРАНСТВО — топологическое пространство, в к ром всякие два множества, из к рых одно замкнуто, а другое состоит лишь из одной точки, функционально отделимы (см. Отделимости аксиомы). В. р. п., в к рых все одноточечные множества замкнуты (т. е. вполне… … Математическая энциклопедия
Регулярное деление плоскости — Эшер, Мауриц Корнелис Регулярное деление плоскости, нидерл. Regelmatige vlakverdeling Ксилография. «Регулярное деление плоскости» серия ксилографий нидерландского художника Эшера, начатая им в 1936 году. В основу этих работ лёг принцип тес … Википедия
КВАЗИНОРМАЛЬНОЕ ПРОСТРАНСТВО — регулярное пространство, в к ром два непересекающихся p множества имеют непересекающиеся окрестности. Всякое Т l пространство, в к ром любые два непересекающихся p множества имеют непересекающиеся окрестности, является К. п. Для К. п. и только… … Математическая энциклопедия
РЕГУЛЯРНОЕ КОЛЬЦО — в к о м м у т а т и в н о й а л г е б р е нётерово кольцо А, все локализации к рого регулярны; здесь простой идеал в А. При этом локальное нётерово кольцо Ас максимальным идеалом наз. р е г у л я р н ы м, если порождается пэлементами, где n=dim A … Математическая энциклопедия
РЕГУЛЯРНОЕ ПРЕДСТАВЛЕНИЕ — 1) P. п. (левое) а л г е б р ы А линейное представление Lалгебры Ав векторном пространстве Е=А, определяемое формулой L(a)b=ab для всех ; аналогично, формула , определяет (анти) представление алгебры Ав пространстве Е=А, наз. (правым) Р. п. А.… … Математическая энциклопедия
МЕТРИЧЕСКОЕ ПРОСТРАНСТВО — множество Xвместе с нек рой метрикойr на ном. Теоретико множественный подход к изучению фигур (пространств) основан на исследовании взаимного расположения составляющих их элементарных частей. Одной из фундаментальных характеристик взаимного… … Математическая энциклопедия
Метризуемое пространство — Метризуемое пространство топологическое пространство, гомеоморфное некоторому метрическому пространству. Иначе говоря, пространство, топология которого порождается некоторой метрикой. Если такая метрика существует, то она не… … Википедия
НУЛЬМЕРНОЕ ПРОСТРАНСТВО — в смысле ind пространство, обладающее базой из множеств одновременно открытых и замкнутых в нем. Каждое дискретное пространство нульмерно, однако Н. п. может не иметь изолированных точек (пример пространство рациональных чисел ). Все нульмерные… … Математическая энциклопедия
и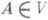 
. Регулярными являются все вполне регулярные пространства и, в частности, все метрические пространства.