- РАСПРЕДЕЛЕНИИ СХОДИМОСТЬ
в основном слабая сходимость и сходимость по вариации, определяемые следующим образом. Последовательность распределений (вероятностных мер) { Р п}. на борелевских множествах метрич. пространства Sназ. с л а б о с х о д я щ е й с я к р а с п р е д е л е н и ю Р, если


для любой действительной ограниченной непрерывной функции f на S. Слабая сходимость является основным типом сходимости, рассматриваемым в теории вероятностей. Обозначают ее обычно знаком
 . Следующие условия равносильны слабой сходимости:
. Следующие условия равносильны слабой сходимости:
1) соотношение (*) выполняется для любой ограниченной равномерно непрерывной действительной функции f;
2) соотношение (*) выполняется для любой ограниченной непрерывной Р-почти всюду действительной функции f;
3)

для любого замкнутого множества FМS;
4)

для любого открытого множества GМS;
5)

для любого борелевского множества AМSтакого, что
 , где
, где  - граница А;
- граница А;
6)

где ресть Леви - Прохорова метрика.
Пусть U- замкнутый относительно пересечений класс подмножеств Sтакой, что всякое открытое множество из Sесть конечное или счетное объединение множеств из U. Тогда если
 при всех
при всех  , то
, то  . Если
. Если  - функции распределения, отвечающие Р n и Рсоответственно, то
- функции распределения, отвечающие Р n и Рсоответственно, то 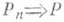 тогда и только тогда, когда
тогда и только тогда, когда  в каждой точке хнепрерывности функции F
в каждой точке хнепрерывности функции F
Пусть пространство Sсепарабельно и
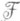 - класс ограниченных борелевских действительных функций на S. Для того чтобы равномерно по
- класс ограниченных борелевских действительных функций на S. Для того чтобы равномерно по  для всякой последовательност
для всякой последовательност  { Р n}такой, что
{ Р n}такой, что  , необходимо и достаточно, чтобы:
, необходимо и достаточно, чтобы:
а)

б)
 где
где

и где Sx,e- открытый шар радиуса e с центром в х. Если класс
 образован индикаторами множеств из нек-рого класса Е, то условия а) и б) сводятся к условию
образован индикаторами множеств из нек-рого класса Е, то условия а) и б) сводятся к условию

где

(когда всякий открытый шар в Sсвязен,

 . Если
. Если  и распределение Р абсолютно непрерывно по мере Лебега, то
и распределение Р абсолютно непрерывно по мере Лебега, то  тогда и только тогда, когда
тогда и только тогда, когда  равномерно по всем борелевским выпуклым множествам А.
равномерно по всем борелевским выпуклым множествам А.
Пусть Р п, Р -- распределения на метрич. пространстве
 и h - непрерывное Р-почти всюду измеримое отображение Sв метрич. пространство
и h - непрерывное Р-почти всюду измеримое отображение Sв метрич. пространство  ; тогда
; тогда  , где для любого распределения Qна Sраспределение Qh -1 есть его h-образ на
, где для любого распределения Qна Sраспределение Qh -1 есть его h-образ на  :
:
 для любого борелевского
для любого борелевского 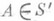
Семейство распределений
 на Sназ. с л а б о о т н о с и т е л ь н о к о м п а к т н ы м, если всякая последовательность его элементов содержит слабо сходящуюся подпоследовательность. Условие слабой относительной компактности дает теорема Прохорова. Семейство
на Sназ. с л а б о о т н о с и т е л ь н о к о м п а к т н ы м, если всякая последовательность его элементов содержит слабо сходящуюся подпоследовательность. Условие слабой относительной компактности дает теорема Прохорова. Семейство  наз. п л о т н ы м, если
наз. п л о т н ы м, если  существует компакт KМS такой, что
существует компакт KМS такой, что  . Т е о р е м а П р о х о р о в а: если
. Т е о р е м а П р о х о р о в а: если  плотно, то оно относительно компактно, а если Sсепарабельно и полно, то слабая относительная компактность
плотно, то оно относительно компактно, а если Sсепарабельно и полно, то слабая относительная компактность  влечет его плотность. В случае, когда
влечет его плотность. В случае, когда  , семейство распределений
, семейство распределений  слабо относительно компактно тогда и только тогда, когда соответствующее
слабо относительно компактно тогда и только тогда, когда соответствующее  семейство характеристич. функций равностепенно непрерывно в нуле.
семейство характеристич. функций равностепенно непрерывно в нуле.
Пусть теперь Р n, Р - распределения на измеримом пространстве (X, А), где Аесть s-алгебра. Под с х о-д и м о с т ь ю по в а р и а ц и и Р n к Р понимают равномерную сходимость по всем множествам из Аили, что равносильно, стремление вариации

к нулю; здесь
 и
и 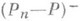 - компоненты разложения Жордана - Хана обобщенной меры Р п --Р.
- компоненты разложения Жордана - Хана обобщенной меры Р п --Р.
Лит.:[1] Б и л л и н г с л и П., Сходимость вероятностных мер, пер. с англ., М., 1977; [2] Л о э в М., Теория вероятностей, пер. с англ., М.. 1962; [3] Б х а т т а ч а р и я Р. Н., Р. Р а н г а Р а о, Аппроксимация нормальным распределением и асимптотические разложения, пер. англ., 1982. В. В. Сазонов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
