РАЗРЕШИМАЯ ФОРМУЛА

(в данной системе) - такая формула Аданной формальной системы, что либо она доказуема в этой системе (т. е. является теоремой), либо опровержима (т. е. доказуемо ее отрицание 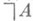). Если всякая замкнутая формула данной формальной системы разрешима в ней, то такая система наз. п о л н о й. (Следует заметить, что нельзя требовать, чтобы в системе были разрешимы все формулы, а не только замкнутые. Так, формула х=0, где х- переменная для натуральных чисел, не выражает ни истинное, ни ложное суждение, и поэтому ни она, ни ее отрицание не являются теоремами формальной арифметики.)

Название "Р. ф." связано с тем, что вопрос об истинности или ложности суждения, выражаемого такой формулой, может быть решен на основе данной системы аксиом. В силу Гёделя теоремы о неполноте в любой формальной системе арифметики найдется неразрешимое предложение, т. е. замкнутая формула, к-рая не является разрешимой в этой системе. В частности, неразрешимой оказывается формула, выражающая утверждение о непротиворечивости такой системы.

Термин "Р. ф." следует отличать от термина "разрешимый предикат". В. Е. Плиско.