РАЗНОСТНАЯ СХЕМА

РАЗНОСТНАЯ СХЕМА

- система разностных уравнений, аппроксимирующих дифференциальное уравнение и дополнительные (начальные, граничные и др.) условия. Аппроксимация исходной дифференциальной задачи Р. с.- это один из способов приближенной дискретизации исходной задачи. Он заключается в том, что заданную область изменения независимых переменных Gзаменяют дискретным множеством точек Gh - с е т к о й, а производные, входящие в дифференциальное уравнение, заменяют на сетке Gh, разностными отношениями. В результате такой замены возникает замкнутая система большого числа алгебраич. уравнений (линейных или нелинейных в зависимости от исходной дифференциальной задачи), к-рая и представляет собой Р. с. По существу Р. с.- это семейство разностных уравнений, зависящих от шагов сетки. Решение Р. с. также зависит параметрически от шагов сетки. Р. с.- многопараметрический и сложный объект. Помимо коэффициентов исходного дифференциального уравнения она содержит свои собственные параметры такие, как шаги по времени и пространству, весовые множители и др. Влияние этих параметров может существенно исказить представление о поведении исходной дифференциальной задачи.

В связи с разностной аппроксимацией дифференциальных задач изучаются следующие вопросы: о способах построения Р. с., о сходимости при измельчении сетки решения разностной задачи к решению исходной дифференциальной задачи, о методах решения систем разностных уравнений. Все перечисленные вопросы рассматривает разностных схем теория. Разработаны эффективные численные методы решения типичных Р. с. для обыкновенных дифференциальных уравнений и уравнений с частными производными, предполагающие использование быстродействующих ЭВМ.

Ниже приводится простой пример Р. с. Пусть имеется дифференциальная задача

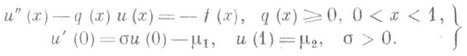(1) Область G{0<x<l} заменяется соткой


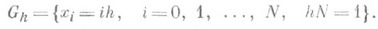
Р. с. для задачи (1) имеет вид

(2)

где . Можно показать, что при решение разностной задачи (2) сходится к решению исходной задачи (1) и при достаточной гладкости функции 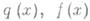Р. с. (2) имеет второй порядок точности, где М - постоянная, не зависящая от h. РешениеР. <с.(2) находится методом прогонки.

Лит.:[1] С а м а р с к и й А. А., Теория разностных схем, М., 1977; [2] С а м а р с к и й А. А., Н и к о л а е в Е. С., Методы решения сеточных уравнений, М., 1978.

А. В. Гулин, А. А. Самарский.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем решить контрольную работу

Полезное


Смотреть что такое "РАЗНОСТНАЯ СХЕМА" в других словарях:

  • Разностная схема — Разностная схема  это конечная система алгебраических уравнений, поставленная в соответствие какой либо дифференциальной задаче, содержащей дифференциальное уравнение и дополнительные условия (например краевые условия и/или начальное… …   Википедия

  • разностная схема конечных элементов — метод конечных элементов — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом Синонимы метод конечных элементов EN finite volume difference schedule …   Справочник технического переводчика

  • Конечно-разностная схема — Разностная схема  это конечная система алгебраических уравнений, поставленная в соответствие какой либо дифференциальной задаче, содержащей дифференциальное уравнение и дополнительные условия (например краевые условия и/или начальное… …   Википедия

  • конечно-разностная схема расчёта на основе контрольных объёмов — (напр. тепломассобмена, теплопроводности) [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN control volume based finite difference schedule …   Справочник технического переводчика

  • Схема — Схема: графический документ [1]; изложение, изображение, представление чего либо в самых общих чертах, упрощённо (например, схема доклада)[2]; электронное устройство, содержащее множество компонентов (интегральная схема). Графический документ… …   Википедия

  • РАЗНОСТНАЯ ВАРИАЦИОННАЯ СХЕМА — разностная схема, построенная на основе вариационной задачи, соответствующей краевой задаче для дифференциального уравнения. Основная идея построения Р. в. с. состоит в том, чтобы при специальном выборе координатных функций в Ритца методе… …   Математическая энциклопедия

  • ГИПЕРБОЛИЧЕСКОГО ТИПА УРАВНЕНИЕ — численные методы решения методы решения уравнений гииерболпч. типа на основе вычислительных алгоритмов. Различные математич. модели во многих случаях приводят к дифференциальным уравнениям гиперболич. типа. Такие уравнения имеют точные аиалитич.… …   Математическая энциклопедия

  • РАЗНОСТНЫХ СХЕМ ТЕОРИЯ — раздел вычислительной математики, изучающий методы приближенного решения дифференциальных уравнений путем их замены конечноразностными уравнениями (р а з н о с т н ы м и с х е м а м и). Р. с. т. изучает способы построения разностных схем,… …   Математическая энциклопедия

  • КРАЕВАЯ ЗАДАЧА — численные методы решения для уравнений с частными производными приближенные методы решения, в результате к рых решение задачи представляется таблицей чисел. Точно решения (в виде явных формул, рядов и т. п.) К. з. можно построить лишь в редких… …   Математическая энциклопедия

  • ГАЗОВОЙ ДИНАМИКИ ЧИСЛЕННЫЕ МЕТОДЫ — методы решения задач газовой динамики на основе вычислительных алгоритмов. Рассмотрим основные аспекты теории численных методов решения задач газовой динамики, записав газовой динамики уравнения в виде законов сохранения в инерциальной… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»