- РАЗЛОЖЕНИЕ ЕДИНИЦЫ
- однопараметрическое семейство
 , проекционных операторов, действующих в гильбертовом пространстве
, проекционных операторов, действующих в гильбертовом пространстве  , такое, что
, такое, что
1)
 , если l<m;
, если l<m;
2) Е l сильно непрерывно слева, т. е. Е l-0 -Еl для любого
 ;
;
3)
 при
при  и
и 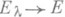 при
при  , здесь О и Е - нулевой и единичный операторы в пространстве
, здесь О и Е - нулевой и единичный операторы в пространстве 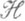 . Условие 2} можно заменить на условие непрерывности справа в каждой точке
. Условие 2} можно заменить на условие непрерывности справа в каждой точке 
Всякий самосопряженный оператор А, действующий в
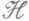 , порождает соответствующее ему вполне определенное Р. е. При этом кроме условий 1)-3) выполняются еще условия:
, порождает соответствующее ему вполне определенное Р. е. При этом кроме условий 1)-3) выполняются еще условия:
4) если В - ограниченный оператор такой, что ВА=АВ, то ВЕl=Еl В для любого А;
5) если А- ограниченный оператор, т, М - его нижняя и верхняя грани соответственно, то
 и Е l=Е при
и Е l=Е при 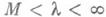
Р. е., порожденное оператором А, полностью определяет спектральные свойства этого оператора, а именно:
(а) точка Кесть регулярная точка оператора Атогда и только тогда, когда она является точкой постоянства, т. е. когда существует d>0 такое, что
 для
для
(Р)
 точка l0 есть собственное значение оператора Атогда и только тогда, когда в этой точке Е l имеет скачок, т. е.
точка l0 есть собственное значение оператора Атогда и только тогда, когда в этой точке Е l имеет скачок, т. е.  ;
;
(у) если
 , то
, то  есть инвариантное подпространство оператора А.
есть инвариантное подпространство оператора А.
Поэтому Р. е., порожденное оператором А, наз. также спектральной функцией этого оператора.
Обратно, каждое Р. е. {Е l} однозначно определяет самосопряженный оператор A, для к-рого это Р. е. является спектральной функцией. Область определения D(А).оператора Асостоит из тех и только тех
 , для к-рых
, для к-рых 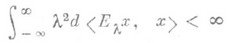 и имеет место представление оператора Ав виде операторного интеграла Стилтьеса
и имеет место представление оператора Ав виде операторного интеграла Стилтьеса

Лит.:[1] Р и с с Ф., С ё к е ф а л ь в и - Н а д ь Б., Лекции по функциональному анализу, пер. с франц., 2 изд., М., 1979; 12] А х и е з е р Н. И., Г л а з м а н И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд., М., I960; [3] К а н т о р о в и ч Л. В., А к и л о в Г. П., Функциональный анализ, 2 изд., М., 1977. В. И. Соболев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
