- КЭЛИ ПРЕОБРАЗОВАНИЕ
линейного (диссипативного) оператора Ас областью определения DomA, плотной в гильбертовом пространстве Н,- оператор
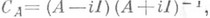определенный на подпространстве 
Матричный вариант такого преобразования рассматривал А. Кэли (A. Cay-ley). К. п. устанавливает соответствие между свойствами операторов А, чей спектр 
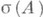"близок" к действительной прямой, и операторов с околоунитарным спектром (близким к окружности 
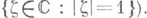Так, имеют место утверждения: 1) если А- линейный диссипатиеный оператор, то С A- сжатие (т. е.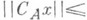
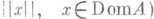и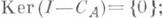 
2) если Т- сжатие, 
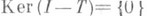и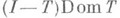 
плотно в Н, то Т=С A при нек-ром линейном диссипативном операторе А:именно .
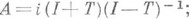3) симметричность Аравносильна изометричности (унитарности) С A; 4) 
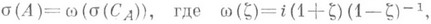в частности ограниченность Аэквивалентна тому, что 
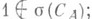51 если 
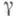- идеал операторов в Н, то из 
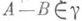следует 
если же А, В - ограниченные операторы, то верно и обратное: из 
следует 
К. п. устанавливает соответствие и между нек-рыми другими характеристиками операторов Аи С А. классификациями частей спектра, кратностями спектров, структурами инвариантных подпространств, функциональными исчислениями, спектральными разложениями и т. д. Так, если А - самосопряженный оператор с разложением единицы 
то 
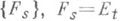при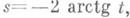 
- разложение единицы для С А и
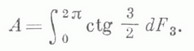
Лит.:[1] А х и е з е р Н. И., Г л а з м а н И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд М. 1966; [2]Секефальви-Надь Б., Ф о я ш Ч., Гармонический анализ операторов в гильбертовом пространстве пер. с англ., М., 1970. Н. <К. Никольский.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
