ПРОДУКТИВНОЕ МНОЖЕСТВО

- множество натуральных чисел А , для к-рого существует такая частично рекурсивная функция j, что 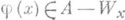для всякого рекурсивно перечислимого множества W_x с геделевым номером х, содержащегося в А. Известно, что для всякого П. м. Асуществует такая общерекурсивная функция y, что уже для каждого хв зависимости от взаимного расположения множеств Аи W_x имеет место либо 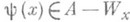, либо 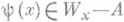. Таким образом, П. <м. "эффективно" отличается от любого рекурсивно перечислимого множества. С другой стороны, всякое П. м. содержит бесконечное рекурсивно перечислимое подмножество, в силу чего П. м. противопоставляются иммунным множествам, хотя иммунными и продуктивными множествами не исчерпывается совокупность множеств, не являющихся рекурсивно перечислимыми. Продуктивными оказываются многие множества, играющие важную роль в рекурсивной теории множеств (напр., множество всех гёделевых номеров общерекурсивных функций в нек-рой гёделевой нумерации всех частично рекурсивных функций) и в ее приложениях (в частности, множества всех номеров истинных и ложных формул элементарной арифметики при естественной нумерации всех ее формул). Рекурсивно перечислимые множества, дополнение к-рых (до натурального ряда) является продуктивным, наз. креативными; они образуют важный класс рекурсивно перечислимых множеств.

Лит.:[1] Роджерс X., Теория рекурсивных функции и эффективная вычислимость, пер. с англ., М., 1972.

В. А. Душский.