ПОСЛЕДОВАТЕЛЬНОСТЕЙ КАТЕГОРИЯ
- ПОСЛЕДОВАТЕЛЬНОСТЕЙ КАТЕГОРИЯ
частный случай общей конструкции категории функторов или категории диаграмм. Пусть  - множество целых чисел, снабженное обычным отношением порядка. Тогда
- множество целых чисел, снабженное обычным отношением порядка. Тогда  можно рассматривать как малую категорию, объектами к-рой являются целые числа, а морфизмами - всевозможные пары вида (i, j), где
можно рассматривать как малую категорию, объектами к-рой являются целые числа, а морфизмами - всевозможные пары вида (i, j), где  и
и  Пара (i, j) - это единственный морфизм объекта iв объект j. Композиция морфизмов определяется следующим равенством: (i, j)(j, k)=(i, k).
Пара (i, j) - это единственный морфизм объекта iв объект j. Композиция морфизмов определяется следующим равенством: (i, j)(j, k)=(i, k).
Для произвольной категории  категория кова-риантных функторов
категория кова-риантных функторов  из
из  в
в 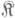 наз. категорией последовательностей над
наз. категорией последовательностей над  Чтобы задать функтор
Чтобы задать функтор  , достаточно указать семейство объектов из
, достаточно указать семейство объектов из  , заиндексированное целыми числами, и для каждой пары объектов А i, Ai+1 выбрать произвольный морфизм
, заиндексированное целыми числами, и для каждой пары объектов А i, Ai+1 выбрать произвольный морфизм  Тогда отображения F(i)=Ai,F(i,i+1)=ai,i+1 однозначно продолжаются до функтора
Тогда отображения F(i)=Ai,F(i,i+1)=ai,i+1 однозначно продолжаются до функтора  . Естественное преобразование j функтора
. Естественное преобразование j функтора  в функтор
в функтор  , т. е. морфизм категории последовательностей, задается таким семейством морфизмов
, т. е. морфизм категории последовательностей, задается таким семейством морфизмов  , что jiG(i,i+1)=F(i,i+1).ji+1 для любого
, что jiG(i,i+1)=F(i,i+1).ji+1 для любого  .
.
Если 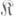 - категория с нулевыми морфизмами, то в П. к.
- категория с нулевыми морфизмами, то в П. к.  выделяется полная подкатегория комплексов, т. е. таких функторов
выделяется полная подкатегория комплексов, т. е. таких функторов  , что F(i, i+1) F(i+1, i+2) = 0 для любого
, что F(i, i+1) F(i+1, i+2) = 0 для любого  . Для абелевой категории
. Для абелевой категории  П. к. и подкатегория комплексов являются абелевыми категориями.
П. к. и подкатегория комплексов являются абелевыми категориями.
Вместо категории  можно рассматривать ее подкатегории, состоящие только из неотрицательных или только из неположительных чисел. Соответствующие категории диаграмм также наз. П. к. М. Ш. Цаленко.
можно рассматривать ее подкатегории, состоящие только из неотрицательных или только из неположительных чисел. Соответствующие категории диаграмм также наз. П. к. М. Ш. Цаленко.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ПОСЛЕДОВАТЕЛЬНОСТЕЙ КАТЕГОРИЯ" в других словарях:
АБЕЛЕВА КАТЕГОРИЯ — категория, обладающая рядом характерных свойств категории всех абелевых групп. А. к. были введены как основа абстрактного построения гомологич. алгебры (см. [4]). Категория наз. абелевой (см. [2]), если она удовлетворяет следующим аксиомам: А0.… … Математическая энциклопедия
Свёртка последовательностей — это результат перемножения элементов двух заданных числовых последовательностей таким образом, что члены одной последовательности берутся с возрастанием индексов, а члены другой с убыванием (что и служит основанием для принятого названия данной… … Википедия
Выравнивание последовательностей — В биоинформатике, выравнивание последовательностей размещение последовательностей ДНК, РНК, и белков для того, чтобы увидеть места схожести, которые могут быть следствием функциональных, структурных или эволюционных взаимосвязей между… … Википедия
Множественное выравнивание последовательностей — (multiple sequence alignment) это выравнение трех и более биологических последовательностей, обычно белков, ДНК, или РНК. Категория: Генетика … Википедия
Числовая последовательность — Последовательность Числовая последовательность это последовательность элементов числового пространства. Числовые пос … Википедия
ГОМОТОПИЧЕСКИЙ ТИП — класс гомотопически эквивалентных топологич. пространств. Отображения и наз. взаимно обратными гомотопическими эквивалентностями, если и Если выполнено только первое из этих соотношений, то gназ. гомотопически мономорфным отображением, а f… … Математическая энциклопедия
Псевдослучайная двоичная последовательность — частный случай ПСП, в которой элементы принимают два возможных значения 0 и 1 (или 1 и +1 ). Постулаты Голомба Одна из первых формулировок некоторых основополагающих правил для статистических свойств периодических псевдослучайных… … Википедия
Псевдослучайный алгоритм — шифрования такой алгоритм шифрования, что каждый блок (символ) исходного текста шифруется своим собственным ключом, причем каждый следующий ключ является следующим членом псевдослучайной последовательности, а основной (базовый) ключ первым… … Википедия
Математика гармонии — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия
Конструктивные способы определения вещественного числа — При конструктивном подходе к определению вещественного числа вещественные числа строят, исходя из рациональных, которые считают заданными. Во всех трёх нижеизложенных способах за основу берутся рациональные числа и конструируются новые объекты,… … Википедия
 - множество целых чисел, снабженное обычным отношением порядка. Тогда
- множество целых чисел, снабженное обычным отношением порядка. Тогда  можно рассматривать как малую категорию, объектами к-рой являются целые числа, а морфизмами - всевозможные пары вида (i, j), где
можно рассматривать как малую категорию, объектами к-рой являются целые числа, а морфизмами - всевозможные пары вида (i, j), где  и
и  Пара (i, j) - это единственный морфизм объекта iв объект j. Композиция морфизмов определяется следующим равенством: (i, j)(j, k)=(i, k).
Пара (i, j) - это единственный морфизм объекта iв объект j. Композиция морфизмов определяется следующим равенством: (i, j)(j, k)=(i, k). категория кова-риантных функторов
категория кова-риантных функторов  из
из  в
в 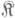 наз. категорией последовательностей над
наз. категорией последовательностей над  Чтобы задать функтор
Чтобы задать функтор  , достаточно указать семейство объектов из
, достаточно указать семейство объектов из  , заиндексированное целыми числами, и для каждой пары объектов А i, Ai+1 выбрать произвольный морфизм
, заиндексированное целыми числами, и для каждой пары объектов А i, Ai+1 выбрать произвольный морфизм  Тогда отображения F(i)=Ai,F(i,i+1)=ai,i+1 однозначно продолжаются до функтора
Тогда отображения F(i)=Ai,F(i,i+1)=ai,i+1 однозначно продолжаются до функтора  . Естественное преобразование j функтора
. Естественное преобразование j функтора  в функтор
в функтор  , т. е. морфизм категории последовательностей, задается таким семейством морфизмов
, т. е. морфизм категории последовательностей, задается таким семейством морфизмов  , что jiG(i,i+1)=F(i,i+1).ji+1 для любого
, что jiG(i,i+1)=F(i,i+1).ji+1 для любого  .
.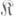 - категория с нулевыми морфизмами, то в П. к.
- категория с нулевыми морфизмами, то в П. к.  выделяется полная подкатегория комплексов, т. е. таких функторов
выделяется полная подкатегория комплексов, т. е. таких функторов  , что F(i, i+1) F(i+1, i+2) = 0 для любого
, что F(i, i+1) F(i+1, i+2) = 0 для любого  . Для абелевой категории
. Для абелевой категории  П. к. и подкатегория комплексов являются абелевыми категориями.
П. к. и подкатегория комплексов являются абелевыми категориями. можно рассматривать ее подкатегории, состоящие только из неотрицательных или только из неположительных чисел. Соответствующие категории диаграмм также наз. П. к. М. Ш. Цаленко.
можно рассматривать ее подкатегории, состоящие только из неотрицательных или только из неположительных чисел. Соответствующие категории диаграмм также наз. П. к. М. Ш. Цаленко.