- ПОСЛЕДОВАНИЯ ОТОБРАЖЕНИЕ
для гладкого или хотя бы непрерывного потока {St} и трансверсальной к нему гиперповерхности V - отображение Т, сопоставляющее точке
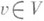 первую по времени точку пересечения с Vисходящей из vположительной полутраектории потока (и определенное для тех v, для к-рых такое пересечение имеется). (Гиперповерхность Vназ. при этом сечением, секущей поверхностью, трансверсалью.) Когда размерность dim V=l (так что {St} - поток на плоскости или двумерной поверхности; в этом случае Vназ. также дугой без контакта) и Vпараметризована числовым параметром s, то смещение точек Vпод действием П. о. описывается нек-рой числовой функцией f одного переменного (если vотвечает значению параметра s, то Tv - значению параметра s+f(s)), к-рая наз. функцией последования. Впервые П. о. использовал А. Пуанкаре (Н. Poincare, [1]), поэтому иногда П. о. наз. отображением Пуанкаре.
первую по времени точку пересечения с Vисходящей из vположительной полутраектории потока (и определенное для тех v, для к-рых такое пересечение имеется). (Гиперповерхность Vназ. при этом сечением, секущей поверхностью, трансверсалью.) Когда размерность dim V=l (так что {St} - поток на плоскости или двумерной поверхности; в этом случае Vназ. также дугой без контакта) и Vпараметризована числовым параметром s, то смещение точек Vпод действием П. о. описывается нек-рой числовой функцией f одного переменного (если vотвечает значению параметра s, то Tv - значению параметра s+f(s)), к-рая наз. функцией последования. Впервые П. о. использовал А. Пуанкаре (Н. Poincare, [1]), поэтому иногда П. о. наз. отображением Пуанкаре.
Если любая полутраектория пересекает V, то П. о. (определенное в данном случае на всем V).в значительной степени определяет поведение всех траекторий потока. Однако такие "глобальные" сечения существуют далеко не всегда (в частности, у гамильтоновой системы на многообразии постоянной энергии, не проходящем через критич. точки гамильтониана, т. е. равнове сия положения, нет заткнутых - как многообразия - глобальных сечений; см. [3] гл. VIII, п. 4.7).
Для неавтономной системы с периодической правой частью
 (*)
(*)
возникает аналог П. о.: точке хсопоставляют точку Tx=j(t, х), где j (t, x) - решение системы (*) с начальным значением j(0, х)=х. Это "отображение сдвига на период" можно даже формально рассматривать как П. о., если (*) рассматривать как автономную систему в "цилиндрическом" фазовом пространстве. Отображение Топределено всюду, если решения системы (*) определены при всех t.
Чаще приходится иметь дело с "локальным" сечением - его пересекает только часть траекторий и нередко только часть пересекающих его траекторий вновь возвращается на V. Примером может служить маленькая гладкая "площадка" коразмерности один, трансверсально пересекающая нек-рую замкнутую траекторию L. В этом случае П. о. определено вблизи
 и характеризует поведение траекторий вблизи L.
и характеризует поведение траекторий вблизи L.
В теории слоений также вводится П. о. (см. [2]), являющееся обобщением предыдущего примера (и охватывающее также П. о. для обыкновенных дифференциальных уравнений в комплексной области).
Лит.:[1] Пуанкаре А., О кривых, определяемых дифференциальными уравнениями, пер. с франц., М., 1947; [2] Тамура И., Топология слоений, пер. с япон., М., 1979; [3] Годбийон К., Дифференциальная геометрия и аналитическая механика, пер. с франц., М., 1973. Д. В. Аносов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
