ПОЛУЛИНЕЙНОЕ ОТОБРАЖЕНИЕ

ПОЛУЛИНЕЙНОЕ ОТОБРАЖЕНИЕ

отображение a (левого) модуля Мв (левый) модуль Nнад одним и тем же кольцом А, удовлетворяющее условиям:


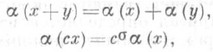
где 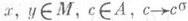- нек-рый автоморфизм кольца А. В этом случае говорят, что а полулинейно относительно автоморфизма s. П. о. векторных пространств над полем С относительно комплексного сопряжения 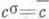наз. также антилинейным отображением. П. о. A-модуля Мв себя наз. полулинейным преобразованием.

Пример. Гомотетия A-модуля М, т. е. отображение 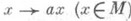, где а - фиксированный обратимый элемент кольца А, есть полулинейное преобразование относительно автоморфизма с а=аса -1.

Для П. о. остаются справедливыми многие свойства линейных отображений и гомоморфизмов модулей. В частности, ядро и образ П. о. являются подмодулями; П. о. свободных модулей с конечными базисами полностью определяются своей матрицей; для П. о. векторных пространств определяется ранг, совпадающий с рангом его матрицы, и т. д.

Лит.:[1] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962. А. Л. Онищик.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно сделать НИР?

Смотреть что такое "ПОЛУЛИНЕЙНОЕ ОТОБРАЖЕНИЕ" в других словарях:

  • ПОЛУТОРАЛИНЕЙНАЯ ФОРМА — функция от двух переменных на модуле (напр., на векторном пространстве), линейная но одному переменному и полулинейная по другому. Точнее, П. ф, на унитарном модуле Енад ассоциативно коммутативным кольцом А с единицей, снабженным автоморфизмом ,… …   Математическая энциклопедия

  • ЛИ p-АЛГЕБРА — ограниченная алгебра Ли, алгебра Lнад полем kхарактеристики р>0 (или, более общо, над кольцом простой характеристики р>0), снабженная р отображением таким, что выполняются следующие соотношения: Здесь внутреннее дифференцирование алгебры L …   Математическая энциклопедия

  • ОРТОГОНАЛЬНАЯ ГРУППА — группа всех линейных преобразований n мерного векторного пространства Vнад полем k, сохраняющих фиксированную невырожденную квадратичную форму Q на V(т. е. таких линейных преобразований j, что Q(jn(v))=Q(v) для любого ). О. г. принадлежит к числу …   Математическая энциклопедия

  • УНИТАРНАЯ ГРУППА — относительно формы f группа Un( К, f) всех линейных преобразований n мерного правого линейного пространства Vнад телом К, сохраняющих фиксированную невырожденную полуторалинейную (относительно инволюции J тела К)форму f на V, т. е. таких что У. г …   Математическая энциклопедия

  • ПРОЕКТИВНОЕ ПРЕОБРАЗОВАНИЕ — взаимно однозначное отображение F .проективного пространства ПД на себя, сохраняющее отношение порядка частично упорядоченного (по включению) множества всех подпространств П n, т. е. отображение П n в себя такое, что 1) если , то ; 2) для каждого …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»