ПОДПРЕДСТАВЛЕНИЕ ПРЕДСТАВЛЕНИЯ
- ПОДПРЕДСТАВЛЕНИЕ ПРЕДСТАВЛЕНИЯ
линейное представление r в инвариантном подпространстве 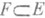 представления пгруппы (алгебры, кольца, полугруппы) X в векторном (топологии. векторном) пространстве Е, определяемое формулой
представления пгруппы (алгебры, кольца, полугруппы) X в векторном (топологии. векторном) пространстве Е, определяемое формулой 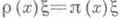 для всех
для всех 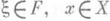 . Если я - непрерывное представление (топологии, группы, алгебры, кольца, полугруппы), то любое его П. п. также непрерывно.
. Если я - непрерывное представление (топологии, группы, алгебры, кольца, полугруппы), то любое его П. п. также непрерывно.
А. И. Штерн.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "ПОДПРЕДСТАВЛЕНИЕ ПРЕДСТАВЛЕНИЯ" в других словарях:
СУЖЕНИЕ ПРЕДСТАВЛЕНИЯ — на инвариантное подпространство то же, что подпредставление представления;С. п. я группы Xна подгруппу Y(алгебры Xна подалгебру Y) представление группы (алгебры) Y, определяемое формулой для всех С. п. наз. также ограничением представления… … Математическая энциклопедия
КВАЗИЭКВИВАЛЕНТНЬЩ ПРЕДСТАВЛЕНИЯ — унитарные представления p1, p2 группы X(или симметричные представления симметричной алгебры X)в гильбертовых пространствах Н 1 и Н 2 соответственно, удовлетворяющие одному из следующих четырех эквивалентных условий: 1) существуют такие унитарно… … Математическая энциклопедия
РАЦИОНАЛЬНОЕ ПРЕДСТАВЛЕНИЕ — а л г е бр а и ч е с к о й г р у п п ы G линейное представление алгебраич. группы G над алгебраически замкнутым полем kв конечномерном векторном пространстве Vнад k, являющееся рациональным (и тем самым регулярным) гомоморфизмом группы Gв GL(V).… … Математическая энциклопедия
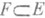 представления пгруппы (алгебры, кольца, полугруппы) X в векторном (топологии. векторном) пространстве Е, определяемое формулой
представления пгруппы (алгебры, кольца, полугруппы) X в векторном (топологии. векторном) пространстве Е, определяемое формулой 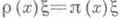 для всех
для всех 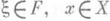 . Если я - непрерывное представление (топологии, группы, алгебры, кольца, полугруппы), то любое его П. п. также непрерывно.
. Если я - непрерывное представление (топологии, группы, алгебры, кольца, полугруппы), то любое его П. п. также непрерывно.