- ПЛОСКОСТЬ
- одно из основных понятий геометрии; обычно косвенным образом определяется аксиомами геометрии. П. может рассматриваться как совокупность двух непересекающихся множеств - множества точек и множества прямых с симметричным отношением инцидентности, связывающим точку и прямую. В зависимости от требований, к-рым удовлетворяет отношение инцидентности, описываемое определенными аксиомами, различают проективные, аффинные, гиперболические, эллиптические П. и др.
П. можно классифицировать по группам коллинеаций (см., напр., [7] гл. 3, где дана классификация Ленца - Бартолоцци проективных и аффинных П.) или по реализации в плоскости тех или иных конфигураций (см., напр., Дезаргова геометрия, Паскалева геометрия).
П. наз. метрической, если кроме отношения инцидентности определено расстояние между любой парой точек. Так, в Гильберта системе аксиом евклидовой геометрии расстояние вводится на базе аксиом конгруэнтности и непрерывности, и П. в этом случае наз. непрерывной (см. [1]). В случае невыполнения для П. аксиом непрерывности П. наз. дискретной (см., напр., Неархимедова геометрия), а П., состоящая из конечного числа точек, а следовательно, и прямых, наз. конечной (см. [7]).
Одним из путей изучения П. является введение в ней координат и тернарной операции с последующим ее изучением (см., напр., [7]), [8]).
В системе аксиом Вейля пространства Е 3 П. является производным понятием от понятий "вектор" и "точка". Под П., проходящей через точку
 и векторы m и n, понимается множество точек таких, что
и векторы m и n, понимается множество точек таких, что
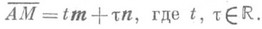
В прямоугольной системе координат ( х, у, z).пространства Е 3 П. задается линейным уравнением
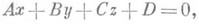
коэффициенты А, В, С определяют координаты нормального вектора этой П. В m-мерном пространстве re-мерные П. описываются системами линейных уравнений (см. [5]).
Взаимное расположение П. в различных m-мерных пространствах определяется соответствующими аксиомами инцидентности так же, как и свойства инцидентности плоскостей и прямых.
Лит.:[1] Гильберт Д., Основания геометрии, пер. с нем., М.- Л., 1948: [2] Ефимов Н. В., Высшая геометрия, 6 изд., М., 1978; [3] Об основаниях геометрии, М., 1956; [4] Бахман Ф., Построение геометрии на основе понятия симметрии, пер. с нем., М., 1969; [5] Донеддю А., Евклидова планиметрия, пер. с франц., М., 1978; [6] Розенфельд Б. А., Многомерные пространства, М., 1966; [7] Dеmbоwski P., Finite geometries, В., 1968; [8] Pikеrt G., Projektive Ebenen, В., 1955. В. В. Афанасьев, Л. А. Сидоров.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
