- ПЛОСКИЙ МОРФИЗМ
- морфизм схем
 такой, что для любой точки
такой, что для любой точки  локальное кольцо
локальное кольцо  является плоским над
является плоским над  (см. Плоский модуль). Вообще, пусть
(см. Плоский модуль). Вообще, пусть  - пучок
- пучок  -модулей, он наз. плоским над Yв точке
-модулей, он наз. плоским над Yв точке  , если
, если  - плоский модуль над кольцом
- плоский модуль над кольцом  . При нек-рых (довольно слабых) условиях конечности множество точек, в к-рых когерентный
. При нек-рых (довольно слабых) условиях конечности множество точек, в к-рых когерентный  -модуль
-модуль  является плоским, открыто в X. Если при этом схема Yцелостна, то существует открытое непустое подмножество
является плоским, открыто в X. Если при этом схема Yцелостна, то существует открытое непустое подмножество  такое, что
такое, что  - П. м. над Yво всех точках, лежащих над U.
- П. м. над Yво всех точках, лежащих над U.
П. м. конечного типа соответствуют интуитивному понятию непрерывного семейства многообразий. П. м. открыт и равноразмерен (т. е. размерность слоев f-1 (у) локально постоянна по
 ). Для многих гео-метрич. свойств множество точек
). Для многих гео-метрич. свойств множество точек 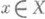 , в к-рых слой f-1(f(x)).плоского морфизма
, в к-рых слой f-1(f(x)).плоского морфизма  обладает этим свойством, открыто в X. Если П. м. f собственный, то открытым является и множество точек
обладает этим свойством, открыто в X. Если П. м. f собственный, то открытым является и множество точек 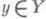 , слои над к-рыми обладают этим свойством (см. [1]).
, слои над к-рыми обладают этим свойством (см. [1]).
П. м. применяются также в теории спуска. Морфизм схем наз. строго плоским, если он плоский и сюръективный. Тогда, как правило, для проверки какого-либо свойства нек-рого объекта над Yдостаточно проверить это свойство для объекта, полученного после строго плоской замены базы
 (см. [1]). В связи с этим представляют интерес критерии плоскостности морфизма
(см. [1]). В связи с этим представляют интерес критерии плоскостности морфизма  (или
(или  -модуля
-модуля  ); при этом Yможно считать локальной схемой. Простейший критерий относится к случаю, когда база Yодномерна и регулярна: когерентный
); при этом Yможно считать локальной схемой. Простейший критерий относится к случаю, когда база Yодномерна и регулярна: когерентный  -модуль
-модуль  будет плоским тогда и только тогда, когда униформизирующая на Yимеет тривиальный аннулятор в
будет плоским тогда и только тогда, когда униформизирующая на Yимеет тривиальный аннулятор в  . Общий случай в нек-ром смысле сводится к одномерному. Пусть Y - приведенная нётерова схема и для любого морфизма
. Общий случай в нек-ром смысле сводится к одномерному. Пусть Y - приведенная нётерова схема и для любого морфизма  , где Z - одномерная регулярная схема, замена базы
, где Z - одномерная регулярная схема, замена базы  является П. м.; тогда f есть П. м. Другой критерий плоскостности требует, чтобы
является П. м.; тогда f есть П. м. Другой критерий плоскостности требует, чтобы  был универсально открыт,
был универсально открыт,
а Y и геометрич. слои
 - приведены.
- приведены.
Лит.:[1] Grothendieck A., Dieudonne .Т., Elements de geometric algebrique, 4, "Publ. math. IHES", 1964, № 24; 1966, № 28; [2] Мамфорд Д., Лекции о кривых на алгебраической поверхности, пер. с англ., М., 1968; [3] Rауnaud M., GrusonL., "Invent, math.", 1971, v. 13, p. 1-89.
В. И. Данилов
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
