- ПЛАНИГОН
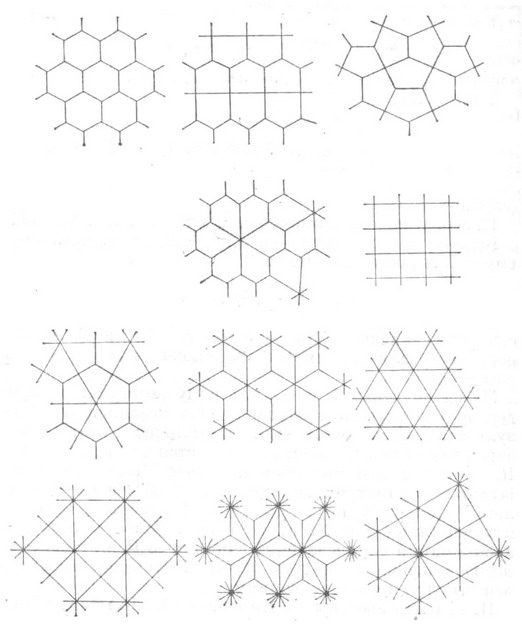
- выпуклый многоугольник правильного разбиения плоскости на равные многоугольники, т. е. такого разбиения, что существует группа движений плоскости, совмещающая разбиение с собой, к-рая действует транзитивно на совокупности многоугольников разбиения. На евклидовой плоскости существует 11 комбинаторных типов разбиения - т. н. сети Шубинкова - Лавеса (см. рис.). Однако группа симметрии для одного комбинаторного типа может действовать по-разному. Взаимосвязь комбинаторного типа и группы симметрии характеризуется т. н. символом смежности. На евклидовой плоскости существует 46 общих правильных разбиений с различным символом смежности.
На плоскости Лобачевского планигонами являются правильные многоугольники с любым числом kсторон и любым данным числом а сходящихся в каждой вершине П. Для числа сторон k=3, 4, 5, 6,>6 можно выбрать такой размер П., что
Многомерным аналогом П. является стереоэдр.
Лит.:[1] Делоне Б. Н., "Изв. АН СССР. Сер. матем.", 1959, т. 23, № 3, с. 365-86; [2] Делоне Б. Н., Долбилин Н. П., Штогрин М. И., "Тр. Матем. ин-та АН СССР", 1978, т. 148, с. 109-40; [3] Узоры симметрии, пер. с англ., М., 1980. А. В. Иванов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
