ПАРАМЕТРИКСА МЕТОД

- один из методов изучения краевых задач для дифференциальных уравнений с переменными коэффициентами с помощью интегральных уравнений.

Пусть в какой-либо области G n -мерного евклидова пространства рассматривается эллиптич. дифференциальный оператор порядка т

В равенстве (1) символом обозначен мультииндекс , где - неотрицательные целые

числа, ,

Каждому оператору (1) сопоставляется однородный эллиптич. оператор

с постоянными коэффициентами, где - произвольная фиксирования точка. Пусть обозначает фундаментальное решение оператора , параметрически зависящее от x₀, тогда функция наз. параметриксом оператора (1) с особенностью в точке х ₀.

В частности, для эллиптич. оператора 2-го порядка

в качестве параметрикса с особенностью в точке y может быть взята функция Леви:

В равенстве (2) , (у) - определитель матрицы ,

- элементы матрицы, обратной к матрице 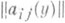Пусть - интегральный оператор

действующий на функциях из , и

Поскольку, в силу определения фундаментального решения,

где I - тождественный оператор, то

Это равенство означает, что для каждой достаточно гладкой и финитной в области G функции справедливо представление

и, кроме того, если

то является решением уравнения

Таким образом, вопрос о локальной разрешимости уравнения сводится к вопросу об обратимости оператора

Если применять оператор к функциям j, к-рые обращаются в нуль вне шара радиуса Rс центром в точке x₀, то при достаточно малом R норма оператора может быть сделана меньше единицы. Тогда будет существовать оператор и, следовательно, оператор , к-рый является обратным к оператору L(x, D). Оператор Еявляется интегральным оператором, ядро к-рого представляет собой фундаментальное решение оператора L(x, D).

Параметриксом иногда наз. не только функцию , но и интегральный оператор с ядром , определенный равенством (3).

В теории псевдодифференциальных операторов вместо оператора параметриксом оператора L(x, D).наз. оператор Sтакой, что I-L(x, D)Sи I-SL(x, D).являются интегральными операторами с бесконечно дифференцируемыми ядрами. Если же таким оператором является лишь оператор I-SL (или I-LS), то Sназ. левым (соответственно правым) параметриксом оператора L(x, D). Иначе говоря, оператор S_x0 в равенстве (4) является левым параметриксом, если оператор в этом равенстве имеет бесконечно дифференцируемое ядро. Если у оператора L(x, D).существуют левый параметрикс S' и правый параметрикс S", то каждый из этих операторов является параметриксом. Существование параметрикса доказано для гипоэллиптических псевдодифференциальных операторов (см. [3]).

Лит.:[1] Берс Л., Джон Ф., Шехтер М.., Уравнения с частными производными, пер. с англ., М., 1966; [2] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [3]Xёрмандер Л., в сб.; Псевдодифференциальные операторы, М., 1967.

Т. А. Алимов.