ОРТОГОНАЛЬНЫЙ ПРОЕКТОР

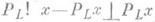, ортопроектор,- отображение P_L гильбертова пространства H на его подпространство Lтакое, что ортогонально . О. п. есть ограниченный самосопряженный оператор, действующий в гильбертовом пространстве H, и такой, что и 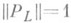Обратно, если дан ограниченный самосопряженный оператор, действующий в гильбертовом пространстве Н, и такой, что Р ²=Р, то 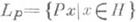является подпространством и Ресть О. п. на L_P. Два О. п. P_L1, P_L2 наз. ортогональными, если ; это эквивалентно условию, что

Свойства О. п.: 1) для того чтобы сумма P_L1+P_L2 двух О. п. была О. п., необходимо и достаточно, чтобы P_L1P_L2=0, в этом случае P_L1+P_L2=P_L1+L22) для того чтобы композиция P_L1P_L2 была О. п., необходимо и достаточно, чтобы P_L1P_L2=P_L2P_L1 в этом случае

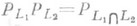
О. п. P_L, наз. частью О. п. P_L, если L' есть подпространство L. При этом P_L -P_L' является О. и. на - ортогональное дополнение к L' в L. В частности, I-P_L есть О. п, на .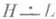

Лит.:[1] Люстерник Л. А., Соболев В. И., Плементы функционального анализа, 2 изд., М., 1965; [2] Ахиезер Н. И., Глазман И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд., М., I960; [3] Рисе Ф., Сёкефальви-Надь Б., Лекции по функциональному анализу, пер. с франц., 2 изд., М., 1979. В. И. Соболев.