ОДНОСТОРОННИЕ И ДВУСТОРОННИЕ ПОВЕРХНОСТИ

- два тина поверхностей, различающихся по способу их расположения в объемлющем пространстве (одностороннее расположение и двустороннее расположение). Напр., цилиндр представляет собой двустороннюю поверхность (д. п.), а Мёбиуса лист- одностороннюю поверхность (о. п.). Характерное отличие этих поверхностей - граница цилиндра состоит из двух кривых, а граница листа Мёбиуса из одной кривой. Среди

замкнутых поверхностей двусторонней является сфера и тор, а односторонней - Клейна поверхность. Примерами двустороннего и одностороннего расположения кривой могут служить вложения окружности в лист Мёбиуса. Так, цикл (см. рис.) является односторонней кривой, а цикл - двусторонней (и вообще, любой дезориентирующий путь лежит в поверхности односторонне).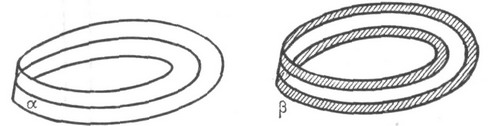

Более точно О. и д. п.- два типа многообразий, различающихся способом вложения их в объемлющее пространство (на единицу большей размерности). Дву-сторонность и односторонность связаны с ориентируемостью и неориентируемостью (см. Ориентация), но в отличие от последних не являются внутренними свойствами поверхности и зависят от объемлющего пространства. Так, напр., существуют ориентируемые д. п.: ; неориентируемые д. п.: ; ориентируемые о. п.:; неориентируемые о. п.: 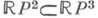(здесь - сфера, - тор, - проективная плоскость, 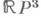- проективное пространство, - дезориентирующий путь на ).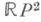

В ориентируемом пространстве (напр., в Rⁿ) гиперповерхность является ориентируемой в том и только в том случае, когда она является д. п.

Пусть вдоль замкнутой кривой на гладкой поверхности, погруженной в нек-рое пространство, обносится нормальный вектор так, чтобы он оставался нормальным. Если при возвращении в исходную точку направление нормали совпадает с исходным независимо от выбора кривой, то поверхность наз. двусторонней; в противном случае (когда нормаль окажется противонаправленной исходной) - односторонней. Более общо, двусторонность расположения поверхности П равносильна тривиальности ее нормального расслоения (в таком расслоении существует ненулевое сечение). Наоборот, нормальное расслоение о. п. нетривиально: существует кривая на П, над к-рой расслоение является листом Мёбиуса.

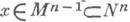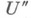Локально всякая (гипер)поверхность в пространстве Nⁿ. разбивает его на две части, т. е. для точки имеется такая окрестность , что Uсостоит из двух компонент и и принадлежит их общей границе. С другой стороны, достаточно тесная окрестность в (если Мзамкнуто в N). имеет либо одну, либо две компоненты, границы к-рых содержат М. В первом случае (гипер) поверхность также наз. односторонней, а во втором - двусторонней. Таким образом, хотя поверхность локально и имеет две стороны, глобально она может быть о. п. и в противоположность д. п. не разбивать свою окрестность в пространстве.

Для д. п. , лежащей в 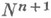, пересечения индекс в N ^{n + 1} для любой замкнутой кривой 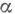на удовлетворяет равенству Если же - о. п., то для нек-рой кривой . Этот факт также можно принять за определение одно- и двусторонности (наряду с обносом нормального вектора и разбиением окрестности).

Лит.:[1] Гильберт Д., Кон-Фоссен С, Наглядная геометрия, пер. с нем., 3 изд., М., 1981; [2] 3ейферт Г., Трельфалль В., Топология, пер. с нем., М.-Л., 1938; [3] Фукс Д. Б..Фоменко А. Т., ГутенмахерВ. <Л., Гомотопическая топология, 2 изд., [М., 1969]. М. И. Войцеховский.