- ОДНОРОДНАЯ ОГРАНИЧЕННАЯ ОБЛАСТЬ
- однородное комплексное многообразие, изоморфное ограниченной области в
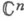 . Примером О. о. о. является "комплексный шар"
. Примером О. о. о. является "комплексный шар"
в к-ром транзитивно действует псевдоунитарная группа SUn ,1 , представленная проективными преобразованиями пространства
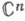 .
.Если D- любая ограниченная область в
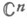 , то эрмитова дифференциальная форма
, то эрмитова дифференциальная форма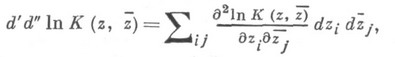
где К- Бергмана кернфункция области D, определяет в Dкэлерову метрику, наз. метрикой Бергмана и инвариантную относительно всех автоморфизмов области D(см. [1], [2]). Группа G(D)всех автоморфизмов области Dявляется вещественной группой Ли, не содержащей нетривиальных связных комплексных подгрупп. Если D- однородна, то метрика Бергмана полна.
Среди О. о. о. выделяются симметрич. области. Ограниченная область Dназ. симметрической, если для любой точки
 существует инволютивный автоморфизм области D, имеющий г изолированной неподвижной точкой. Всякая симметрич. область однородна и является эрмитовым симметрич. пространством относительно метрики Бергмана. Получена [3] классификация симметрич. областей. Имеются 4 серии неприводимых симметрич. областей, связанных с классич. простыми группами Ли, и две особые области размерностей 16 и 27. К числу классических симметрич. областей относятся, в частности, комплексный шар и верхняя полуплоскость Зигеля (см. Зигеля область). Всякая симметрич. область изоморфна прямому произведению неприводимых симметрич. областей [1].
существует инволютивный автоморфизм области D, имеющий г изолированной неподвижной точкой. Всякая симметрич. область однородна и является эрмитовым симметрич. пространством относительно метрики Бергмана. Получена [3] классификация симметрич. областей. Имеются 4 серии неприводимых симметрич. областей, связанных с классич. простыми группами Ли, и две особые области размерностей 16 и 27. К числу классических симметрич. областей относятся, в частности, комплексный шар и верхняя полуплоскость Зигеля (см. Зигеля область). Всякая симметрич. область изоморфна прямому произведению неприводимых симметрич. областей [1].Всякая О. о. о. размерности
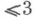 является симметрической [3]. Начиная с размерности 4, существуют и несимметрические О. о. о. (см. [4]). Более того, при
является симметрической [3]. Начиная с размерности 4, существуют и несимметрические О. о. о. (см. [4]). Более того, при  имеется континуум n-мерных О. о. о., среди к-рых лишь конечное число симметрических. Каждая О. о. о. гомеоморфна клетке и аналитически изоморфна аффинно однородной области Зигеля, определенной однозначно с точностью до аффинного изоморфизма. Классификация О. о. о. производится алгебраич. средствами [5].
имеется континуум n-мерных О. о. о., среди к-рых лишь конечное число симметрических. Каждая О. о. о. гомеоморфна клетке и аналитически изоморфна аффинно однородной области Зигеля, определенной однозначно с точностью до аффинного изоморфизма. Классификация О. о. о. производится алгебраич. средствами [5].С О. о. о. связаны многомерные обобщения эйлеровых интегралов (интегралы Зигеля 1-го и 2-го рода), а также гипергеометрич. функции [6].
Лит.:[1] Хелгасон С, Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 19В4; [2] Фукс Б. А., Специальные главы теории аналитических функций многих комплексных переменных, М., 1963; [3] Саrtan E., "Abh. Math. Sem. Hamb. Univ.", 1936, Bd 11, S. 116-62; [4] Пятецкий-Шапиро И. И., Геометрия классических областей и теория автоморфных функций, М., 1961; [5] Винберг Э. Б., Гиндикин С. Г., Пятецкий-Шапиро И. И., "Тр. Моск. матем. об-ва", 1963, т. 12, с. 359-88; [6] Гиндикин С. Г., "Успехи матем. наук", 1964, т. 19, в. 4, с. 3-92.
Д. Б. Винберг.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
