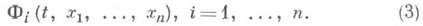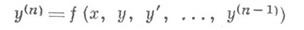Общий интеграл — обыкновенного дифференциального уравнения F (x, у, у ,..., y (n)) =0 соотношение Φ(х, у, C1,..., Cn) =0, содержащее и существенных произвольных постоянных C1,..., Cn, следствием которого является данное … Большая советская энциклопедия
ИНТЕГРАЛ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ — решение дифференциального уравнения. И. д. у. наз. преимущественно соотношение вида Ф( х, у)=0, определяющее решение уобыкновенного дифференциального равнения как неявную функцию независимой переменной х. В этом случае говорят также о частном… … Математическая энциклопедия
Интеграл Лагранжа — Интеграл Коши Лагранжа интеграл уравнений движения идеальной жидкости (уравнений Эйлера) в случае потенциальных течений. Содержание 1 Варианты названия 2 Историческая справка … Википедия
Интеграл Даниэля — Одна из основных трудностей в использовании традиционного интеграла Лебега состоит в том, что его применение требует предварительной разработки подходящей теории меры. Существует другой подход, изложенный Даниэлем (Daniell) в 1918 году в его… … Википедия
Интеграл Даниеля — Одна из основных трудностей в использовании традиционного интеграла Лебега состоит в том, что его применение требует предварительной разработки подходящей теории меры. Существует другой подход, изложенный Даниелем (англ.) в 1918 году в его… … Википедия
Интеграл Шварца — Кристоффеля — Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном отображении… … Википедия
ДАНЖУА ИНТЕГРАЛ — 1) Данжуа узкий (специальный) интеграл обобщение понятия интеграла Лебега. Функция f(x). наз. интегрируемой в смысле узкого (специального, D*) интеграла Данжуа на [ а, b], если существует такая непрерывная функция F(x)на [ а, b], что F… … Математическая энциклопедия
Первый интеграл — системы обыкновенных дифференциальных уравнений , i = 1, …, n соотношение вида (где С произвольная постоянная), левая часть которого сохраняет постоянное значение при подстановке любого решения… … Большая советская энциклопедия
Фазовый интеграл — (англ. Phase Integral) один из фундаментальных интегралов квантовой механики, впервые предложенный Фейнманом в начале 60 х годов XX века. Подобно интегралу по траекториям, этот интеграл позволяет находить смещение фазы, обусловленное… … Википедия
Интегрирование дифференциальных уравнений — (определение и разделение на категории см. Дифференциальные уравнения) общий вид обыкновенного дифференциального уравнения с одной независимой переменной х и с одной искомой функцией у от этой переменной есть f(x, y, y , y ... y(n)) = 0... (*)… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

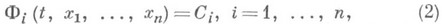
 и в неявном виде описывающая семейство функций, составляющих общее решение этой системы в области G. Часто О. и. системы (1) наз. не соотношения (2), а совокупность функций
и в неявном виде описывающая семейство функций, составляющих общее решение этой системы в области G. Часто О. и. системы (1) наз. не соотношения (2), а совокупность функций