- НИКОЛЬСКОГО ПРОСТРАНСТВО
- банахово пространство
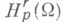 , состоящее из функций, определенных на открытом множестве
, состоящее из функций, определенных на открытом множестве  n-мерного евклидова пространства
n-мерного евклидова пространства 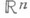 и обладающих определенными разностно-дифференциальными свойствами, характеризующимися вектором
и обладающих определенными разностно-дифференциальными свойствами, характеризующимися вектором 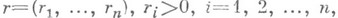 в метрике
в метрике 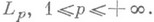 Введены С. М. Никольским.
Введены С. М. Никольским.Н. п.
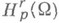 можно описать в терминах свойств разностей от частных производных порядка
можно описать в терминах свойств разностей от частных производных порядка 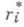 по переменной
по переменной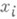 , где
, где 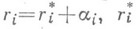 - целое,
- целое,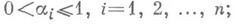
если через
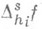 обозначить разность порядка
обозначить разность порядка 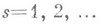 с шагом
с шагом 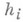 по переменной xi функции f, то
по переменной xi функции f, то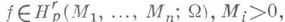
тогда и только тогда, когда функция f имеет в W обобщенные частные производные

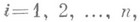 и при
и при 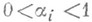 имеет место неравенство
имеет место неравенство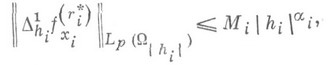
а при
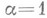 - неравенство
- неравенство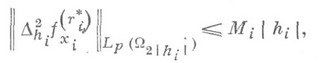
где
 - множество точек
- множество точек  удаленных от границы множества
удаленных от границы множества  больше чем на
больше чем на  - произвольно.
- произвольно.Пространство
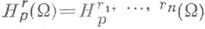 определяется как объединениевсех
определяется как объединениевсех  при всевозможных
при всевозможных 
Если
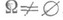 , то при любых
, то при любых 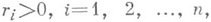
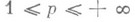 Н. п.
Н. п.  не пусто и в нем существуют функции, не принадлежащие Н. п.
не пусто и в нем существуют функции, не принадлежащие Н. п. ни при каком
ни при каком 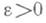 и ни при каком i=l, 2, ..., п.
и ни при каком i=l, 2, ..., п.В случае
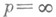 , не целых ri и непрерывности рассматриваемых производных Н. п. является гёльдеровым пространством. Понятие Н. п. обобщается на случай функций, определенных на достаточно гладких многообразиях (см. [2]).
, не целых ri и непрерывности рассматриваемых производных Н. п. является гёльдеровым пространством. Понятие Н. п. обобщается на случай функций, определенных на достаточно гладких многообразиях (см. [2]).Имеется описание Н. п.
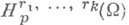 в терминах свойств разностей от частных производных, меньших чем
в терминах свойств разностей от частных производных, меньших чем 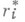 порядков, в частности в терминах свойств разностей достаточно высокого порядка от самой функции.
порядков, в частности в терминах свойств разностей достаточно высокого порядка от самой функции.Пусть
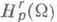 - изотропное пространство, т. е. r1= ... = rn=r. Если область
- изотропное пространство, т. е. r1= ... = rn=r. Если область 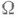 такова, что любую функцию f класса
такова, что любую функцию f класса 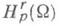 можно продолжить с сохранением класса на все пространство
можно продолжить с сохранением класса на все пространство 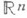 , т. е. так, что продолженная функция будет принадлежать классу
, т. е. так, что продолженная функция будет принадлежать классу 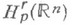 (это всегда имеет место, если граница области достаточно гладкая), то для того, чтобы
(это всегда имеет место, если граница области достаточно гладкая), то для того, чтобы 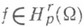 , необходимо и достаточно, чтобы для любых целых неотрицательных к ч s таких, что
, необходимо и достаточно, чтобы для любых целых неотрицательных к ч s таких, что 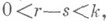 у функции f существовали все частные производные
у функции f существовали все частные производные 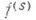 порядка s и существовала постоянная
порядка s и существовала постоянная  для к-рой выполнялись неравенства
для к-рой выполнялись неравенства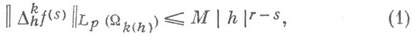
где
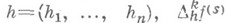 - разность k- гопорядка с векторным шагом hот функции
- разность k- гопорядка с векторным шагом hот функции  . Условие (1) эквивалентно аналогичному условию для модуля непрерывности производной
. Условие (1) эквивалентно аналогичному условию для модуля непрерывности производной 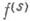 : существует такое M>0, что
: существует такое M>0, что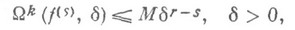
где
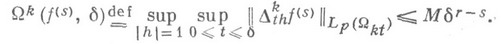
Если для функции
 через Mf обозначить нижнюю грань всех M, для к-рых выполняется условие (1) для всех
через Mf обозначить нижнюю грань всех M, для к-рых выполняется условие (1) для всех  и всех частных производных допустимого порядка .s, то
и всех частных производных допустимого порядка .s, то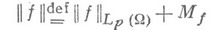
является нормой в Н. п.
 , причем нормы, получающиеся при различных допустимых парах k, s, эквивалентны между собой.
, причем нормы, получающиеся при различных допустимых парах k, s, эквивалентны между собой.Н. п., состоящее из функций, определенных на всем пространстве
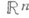 , можно охарактеризовать в терминах наилучших приближений функций из этого пространства с помощью целых функций экспоненциального типа. Пусть
, можно охарактеризовать в терминах наилучших приближений функций из этого пространства с помощью целых функций экспоненциального типа. Пусть  - наилучшее приближение в метрике Lp(Rn )функций
- наилучшее приближение в метрике Lp(Rn )функций  при помощи целых функций
при помощи целых функций  экспоненциального типа степеней
экспоненциального типа степеней 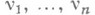 соответственно по переменным
соответственно по переменным  . Для Н. п. справедливы следующие прямая и обратная теоремы типа теорем Бернштейна, Джексона, Зигмунда.
. Для Н. п. справедливы следующие прямая и обратная теоремы типа теорем Бернштейна, Джексона, Зигмунда.Если функция
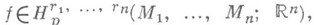 то для любых
то для любых 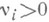 выполняется неравенство
выполняется неравенство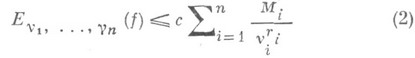
(постоянная с>0 не зависит от функции f).
Наоборот, если для функции
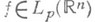 выполняется неравенство (2) для
выполняется неравенство (2) для 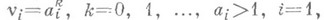 2, ..., п, и qявляется целой функцией степени единица по каждой из переменных
2, ..., п, и qявляется целой функцией степени единица по каждой из переменных  для к-рой
для к-рой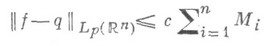
(она существует в силу (2) при k=0), то
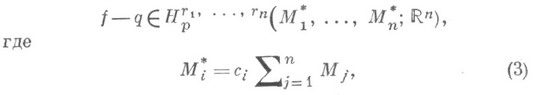
причем постоянные с>0 в (2) и с i>0 в (3) не зависят от M i , i=l, 2, ..., п.
В случае периодической по всем переменным функций f аналогичное описание Н. п. делается посредством наилучших приближений функций через тригонометрия, полиномы вместо целых функций экспоненциального типа (см. 11], [4]).
Н. п. могут быть описаны с помощью оператора Бесселя - Макдональда, применяемого к нек-рому классу обобщенных функций (см. Вложения теоремы).
Для пространств
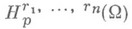 С. М. Никольским доказаны транзитивные теоремы вложения для разных размерностей и метрик (см. [3] и Вложения теоремы), перенесенные в дальнейшем на более общие классы функций. Эти теоремы показывают, что Н. п. образуют замкнутую систему относительно граничных значений входящих в них функций: следы функций из Н. п. на гладких многообразиях в определенном смысле полностью описываются в терминах Н. п.
С. М. Никольским доказаны транзитивные теоремы вложения для разных размерностей и метрик (см. [3] и Вложения теоремы), перенесенные в дальнейшем на более общие классы функций. Эти теоремы показывают, что Н. п. образуют замкнутую систему относительно граничных значений входящих в них функций: следы функций из Н. п. на гладких многообразиях в определенном смысле полностью описываются в терминах Н. п.Свойства Н. п. дали возможность получить необходимые и достаточные условия разрешимости Дирихле задачи в соответствующих Н. п. в терминах принадлежности граничной функции также к нек-рому Н. п.: для того чтобы гармонич. функция ипринадлежала классу
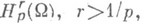 где
где 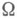 - ограниченная область в
- ограниченная область в 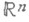 с достаточно гладкой границей
с достаточно гладкой границей  необходимо и достаточно, чтобы граничные значения
необходимо и достаточно, чтобы граничные значения  принадлежали к классу
принадлежали к классу 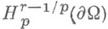 . Отсюда при
. Отсюда при 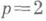 следует, в частности, что если
следует, в частности, что если 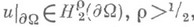 то Дирихле интеграл
то Дирихле интеграл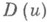 от функции ино области
от функции ино области 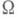 конечен и потому задачу Дирихле можно решить прямым вариационным методом. Из теорем вложения для Н. п. следует, что если для функции иее интеграл Дирихле по области
конечен и потому задачу Дирихле можно решить прямым вариационным методом. Из теорем вложения для Н. п. следует, что если для функции иее интеграл Дирихле по области 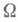 конечен, то
конечен, то 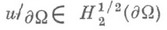 (см. [6]).
(см. [6]).Обобщением Н. п. является пространство Бесова
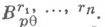
Лит.:[1] Никольский С. М., "Тр. Матем. ин-та АН СССР", 1951, т. 38, с. 244 - 78; [2] его же, "Матем. сб.", 1953, т. 33, № 2, с. 261-326; [3] его же, "Докл. АН СССР", 1958, т. 118, № 1, с. 35-37; [4] его же, Приближение функций многих переменных и теоремы вложения, 2 изд., М., 1977; [5] Бесов О. В., Ильин В. П., Никольский С. М., Интегральные представления функций и теоремы вложения, М., 1975; [6] Никольский С. М., "Докл. АН СССР", 1953, т. 88, в. 3, с. 409 - 11.
Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
