- АФФИННОЕ МНОГООБРАЗИЕ
аффинное алгебраическое многообразие,- обобщение понятия аффинного алгебраического множества. А. м. есть приведенная аффинная схема X конечного типа над полем k, т. е.
 , где А - коммутативная fe-алгебра конечного типа без нильпотентных элементов. А. м.
, где А - коммутативная fe-алгебра конечного типа без нильпотентных элементов. А. м. - кольцо многочленов над полем k, наз. аффинным пространством над kи обозначается
- кольцо многочленов над полем k, наз. аффинным пространством над kи обозначается  . Аффинная схема является А. м. тогда и только тогда, когда она изоморфна приведенной замкнутой подсхеме аффинного пространства. Каждая система образующих
. Аффинная схема является А. м. тогда и только тогда, когда она изоморфна приведенной замкнутой подсхеме аффинного пространства. Каждая система образующих  k-алгебры Аопределяет сюръективный гомоморфизм
k-алгебры Аопределяет сюръективный гомоморфизм  определяемый формулой
определяемый формулой 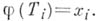 Пусть
Пусть  - алгебраич. замыкание поля k. Подмножество множества
- алгебраич. замыкание поля k. Подмножество множества  , состоящее из общих нулей всех многочленов идеала
, состоящее из общих нулей всех многочленов идеала  , является аффинным алгебраич. множеством над полем k. Координатное кольцо такого аффинного алгебраич. множества изоморфно кольцу А. В свою очередь каждое аффинное алгебраич. множество Xнад полем kопределяет А. м.
, является аффинным алгебраич. множеством над полем k. Координатное кольцо такого аффинного алгебраич. множества изоморфно кольцу А. В свою очередь каждое аффинное алгебраич. множество Xнад полем kопределяет А. м.  , где
, где  - координатное кольцо
- координатное кольцо  . При этом множество точек А. м. находится во взаимно однозначном соответствии с неприводимыми подмногообразиями соответствующего аффинного алгебраич. множества.
. При этом множество точек А. м. находится во взаимно однозначном соответствии с неприводимыми подмногообразиями соответствующего аффинного алгебраич. множества.
С каждым А. м.
 связан функтор на категории k-алгебр, определяемый соответствием
связан функтор на категории k-алгебр, определяемый соответствием

В случае, когда
 (соответственно
(соответственно  ), элементы множества
), элементы множества  (соответственно
(соответственно  ) наз. геометрическим и (соответственно рациональными) точками А. м. X. Множество
) наз. геометрическим и (соответственно рациональными) точками А. м. X. Множество  находится в биективном соответствии с множеством максимальных идеалов
находится в биективном соответствии с множеством максимальных идеалов  кольца
кольца  , а также с множеством точек любого аффинного алгебраич. множества
, а также с множеством точек любого аффинного алгебраич. множества  , координатное кольцо к-рого изоморфно
, координатное кольцо к-рого изоморфно  . При этом спектральная топология в пространстве
. При этом спектральная топология в пространстве  индуцирует на всюду плотном подмножестве
индуцирует на всюду плотном подмножестве  топологию, к-рая соответствует топологии Зариского на V.
топологию, к-рая соответствует топологии Зариского на V.
И. В. Долгачее.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
