НЕПРЕРЫВНЫЙ ФУНКТОР

- синоним понятия "функтор, перестановочный с пределами". Пусть и - категории с пределами. Одноместный ковариант-ный функтор наз. непрерывным, если для любой диаграммы с произвольной малой схемой выполнено равенство .Более подробно последнее равенство означает следующее: если () - предел диаграммы J, причем - морфизмы, входящие в определение предела, то предел диаграммы . Функтор непрерывен тогда и только тогда, когда он перестановочен с произведениями любых семейств объектов и ядрами пар морфизмов. Всякий основной функтор из категории 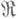в категорию множеств непрерывен.

M. Ш. Цаленко.