- НЕПРЕРЫВНЫЙ ПОТОК
- 1) Н. п. в эргодической теории- такое семейство
 (tпробегает действительную ось
(tпробегает действительную ось 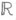 ) автоморфизмов по mod 0 пространства с мерой
) автоморфизмов по mod 0 пространства с мерой  , что: а) при любых равенство
, что: а) при любых равенство 
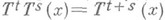 имеет место для всех
имеет место для всех  , кроме, быть может, тех х, к-рые принадлежат нек-рому исключительному множеству меры нуль (оно может зависеть от t, s);иначе говоря,
, кроме, быть может, тех х, к-рые принадлежат нек-рому исключительному множеству меры нуль (оно может зависеть от t, s);иначе говоря, 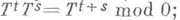 б) для любого измеримого
б) для любого измеримого  мера симметрич. разности
мера симметрич. разности  непрерывно зависит от
непрерывно зависит от  . Пусть
. Пусть 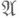 - совокупность всех автоморфизмов mod 0 пространства
- совокупность всех автоморфизмов mod 0 пространства  с обычным отождествлением: если Ти Sсовпадают почти всюду, то они определяют один и тот же элемент из
с обычным отождествлением: если Ти Sсовпадают почти всюду, то они определяют один и тот же элемент из 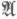 . Если
. Если  снабдить слабой топологией (см. [1]), то условие б) означает непрерывность отображения
снабдить слабой топологией (см. [1]), то условие б) означает непрерывность отображения  , переводящего
, переводящего 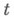 в
в 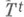 Если
Если  - Лебега пространство, то понятие Н. п. практически совпадает с понятием измеримого потока:последний всегда есть Н. п. (см. [2]), а для любого Н. п.
- Лебега пространство, то понятие Н. п. практически совпадает с понятием измеримого потока:последний всегда есть Н. п. (см. [2]), а для любого Н. п.  существует такой измеримый поток
существует такой измеримый поток 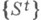 , что
, что  mod 0 при всех t(см. [3]; родственный результат доказан в [4], см. также исправление в [5]). Обращение к тому или иному из этих понятий зависит от характера рассматриваемого вопроса и используемых приемов.
mod 0 при всех t(см. [3]; родственный результат доказан в [4], см. также исправление в [5]). Обращение к тому или иному из этих понятий зависит от характера рассматриваемого вопроса и используемых приемов.2) В другом смысле термин "Н. п." может употребляться с целью подчеркнуть, что рассматриваемый поток относится к топологической динамике. В этом смысле Н. н. есть такая совокупность гомеоморфизмов
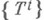 топологич. пространства М, что
топологич. пространства М, что  для всех
для всех  отображение
отображение 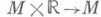 , переводящее
, переводящее  непрерывно.
непрерывно.Во избежание смешения с п. 1) лучше в данном случае говорить о топологическом потоке; а в п. 1)- о метрической непрерывности.
Лит.:[1] Xалмош П. Р., Лекции по эргодической теории, пер. с англ., М., 1959; [2] Хопф Э., "Успехи матем. наук", 1949, т. 4, в. 1, с. 113-82; [3] Вершик А. М., "Изв. АН СССР. Сер. матем.", 1965, т. 29, № 1, с. 127-36; [4] Маскеу G. W., "Illinois J. Math.", 1962, v. 6, № 2, p. 327-35; [5] Ramsay A., "Advances Math.", 1971, v. 6, № 3, p. 253- 322. Д. В. Аносов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
