НЕИЗМЕРИМОЕ МНОЖЕСТВО

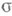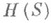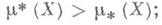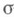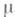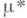- множество, не являющееся измеримым множеством. Подробнее: множество X, принадлежащее наследственному -кольцу , неизмеримо, если здесь Sесть -кольцо, на к-ром задана мера , а и 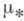- внешняя и внутренняя меры соответственно (см. Мера).

Для интуитивного овладения понятием Н. м. полезно следующее "эффективное построение" его.

Пример 1. Пусть

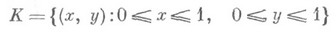
- единичный квадрат,

- множество,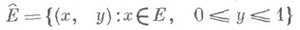соответствующее измеримому по Лебегу множеству Емеры , и пусть . Тогда множество будет Н. м., причем

Наиболее ранняя и простейшая конструкция Н. м. принадлежит Дж. Витали (G. Vitali, 1905).

Пример 2. Пусть - множество всех рациональных чисел. Тогда множество X(множество Витали), имеющее согласно аксиоме выбора с каждым из множеств вида 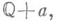где - любое действительное число, ровно по одному общему элементу, является Н. м. Ни одно из множеств Витали не обладает Бэра свойством.

Пример 3. Пусть В, (С)- множество чисел вида 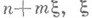- иррациональное число, то, п - целые, с четным п(с нечетным га), а - множество, полученное также с помощью аксиомы выбора из классов эквивалентности множества действительных чисел по отношению:

Пусть 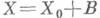. Тогда для всякого измеримого множества Еимеют место равенства:

На возможности ввести полное упорядочение во множестве мощности континуума основана еще одна конструкция Н. м.

Пример 4. Существует множество 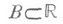такое, что и 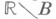пересекаются с каждым несчетным замкнутым множеством. Любое такое множество (множество Бернштейна) неизмеримо (и не обладает свойством Бэра). В частности, любое множество положительной внешней меры содержит Н. м.

Помимо инвариантности относительно сдвига (пример 2) и топологич. свойств (пример 3) есть причины и теоретико-множественной природы, по к-рым невозможно определить нетривиальную меру для всех подмножеств данного множества, в этом, напр., состоит теорема Улама (см. [2]) для множеств ограниченной мощности.

Неизвестен (1982) ни один конкретный пример Н. м., для построения к-рого не использовалась бы аксиома выбора.

Лит-:[1] Халмош П., Теория меры, пер. с англ., М., 1953; [2] Окстоби Д ж., Мера и категория, пер. с англ., М., 1974; [3] Гелбаум В., Олмстед Дж., Контрпримеры в анализе, пер. с англ., М., 1967.

М. И. Войцеховский.