НЕГОЛОНОМНЫЕ СИСТЕМЫ

- системы материальных точек, стесненные связями, среди к-рых имеются кинематич. связи, накладывающие ограничения на скорости (но не на положения) точек системы в ее возможных положениях (см. Голономная система), задаваемые неинтегрируемыми дифференциальными соотношениями вида

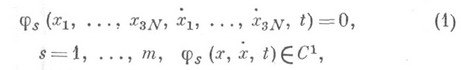
к-рые не могут быть заменены эквивалентными конечными соотношениями между координатами. Здесь 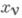- декартовы координаты точек, t- время, N - число точек системы. В большинстве случаев рассматриваются линейные относительно скоростей дx_i / дt связи (1) вида

Связи (1) наз. стационарными, если 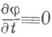. Связи (1) налагают ограничения также на ускорения точек системы вида

Следуя Н. Г. Четаеву [2], принимают, что возможные перемещения систем, стесненных нелинейными связями (1), удовлетворяют условиям вида

В случае линейных связей отсюда следуют общепринятые соотношения

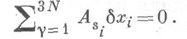
В отличие от голономных систем перемещение между соседними бесконечно близкими возможными положениями Н. с. может быть невозможным (см. [1]).

В обобщенных лагранжевых координатах уравнения (1) и (2) записываются в виде

Для Н. с. число п- тее степеней свободы меньше числа пнезависимых координат 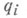на число тнеинтегрируемых уравнений связей.

Выведено много различных видов дифференциальных уравнений движения Н. с, напр. Лагранжа уравнения первого рода, Аппеля уравнения в лагранжевых координатах и квазикоординатах, уравнения Чаплыгина и Воронца в лагранжевых координатах, Больцмана уравнения и уравнения Гамеля в квазикоординатах и др. (см. [3]).

Для Н. с. характерно, что в число дифференциальных уравнений их движения в общем случае входят уравнения связей.

Лит.:[1] Hertz H., Gesammelte Werke, Bd 3 - Die Prinzipien der Mechanik, Lpz., 1894; в рус. пер.- Принципы механики, изложенные в новой связи, М., 195 9; [2] Четаев Н., "Изв. Физ.-матем. об-ва при Казан, ун-те",(3), 1932, т. 6, с. 68-71; [3] Неймарк Ю. И., Фуфаев Н. А., Динамика неголономных систем, М., 1967.

В. В. Румянцев.