НАКРЫВАЮЩАЯ ГОМОТОПИЯ

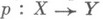для гомотопии F_t отображения при заданном отображении - гомотопия такая, что 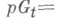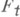. При этом, если накрывающее отображение G_o для отображения F_o было задано заранее, то G_t продолжает G_o. Аксиома накрывающей гомотопии в сильной форме требует, чтобы для данного отображения 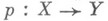любой гомотопии 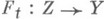с паракомпактным Zи любого имелось бы продолжение G_o до Н. г. G_t. В этом случае рназ. расслоением Гуревича. Наиболее важным примером их служат локально тривиальные расслоения. Если в этом определении требовать лишь, чтобы Zбыло конечным полиэдром, то рназ. расслоением Серра.

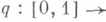
Пусть Xи Y линейно связны и р _A - пространство путей в А(т. е. непрерывных отображений 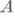). Пусть задано непрерывное отображение где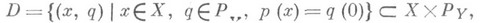 и такое, что 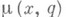начинается в точке хи накрывает q.

Тогда формула 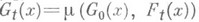дает продолжение накрывающего отображения G_o до Н. г. G_t. В частности, такое отображение Мединственным образом определяется для накрытий, а также для гладкого векторного расслоения с фиксированной связностью. Выполнение аксиомы Н. г. в форме Серра позволяет построить точную гомотопич. последовательность расслоения (см. Гомотопическая группа).

А. В. Чернявский.