- МАРЦИНКЕВИЧА ПРОСТРАНСТВО
банахово пространство My всех измеримых на полуоси
 функций (классов) с конечной нормой
функций (классов) с конечной нормой

где х*(s) - перестановка функции x(t), т. е. невозрастающая непрерывная слева функция, равноизме-рпмая с |x(t)|, а y(t)- нек-рая положительная неубывающая на
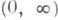 функция, для к-рой y(t)/t не возрастает (в частности, y(t).- неубывающая вогнутая функция); введено И. Марцинкевичем [1].
функция, для к-рой y(t)/t не возрастает (в частности, y(t).- неубывающая вогнутая функция); введено И. Марцинкевичем [1].
Если y(t) ограничена снизу и сверху положительными константами, то пространство My изоморфно L1. Во всех других случаях оно не сепарабельно. Пространство My является интерполяционным между L1 и
 с интерполяционной константой 1.
с интерполяционной константой 1.
На пространстве My определен функционал

к-рый всегда не превосходит
 Функционал F(х).не обладает свойствами нормы; он эквивалентен норме
Функционал F(х).не обладает свойствами нормы; он эквивалентен норме  тогда и только тогда, когда при s>1
тогда и только тогда, когда при s>1

(в частности, для
 ).
).
Пространство My возникло впервые в интерполяционной теореме Марцинкевича (с функционалом F(х)).и связано с интерполированием операторов слабого типа. Оно обладает экстремальным свойством: является наиболее широким среди всех симметричных пространств Е, для к-рых фундаментальная функция совпадает с h/y(h), т. е.
 где
где 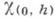 - характеристич. функция интервала (0, h). Если
- характеристич. функция интервала (0, h). Если

то My изоморфно (изометрично, если y вогнута) сопряженному пространству к пространству Лоренца с нормой
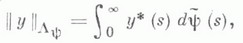
где
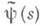 - наименьшая вогнутая мажоранта y(s). При условиях (2) в My выделяется подпространство
- наименьшая вогнутая мажоранта y(s). При условиях (2) в My выделяется подпространство  состоящее из всех функций из My, для к-рых
состоящее из всех функций из My, для к-рых

Если, кроме того,

то подпространство
 совпадает с замыканием в My множества всех финитных ограниченных функций. При этом сопряженное к пространству
совпадает с замыканием в My множества всех финитных ограниченных функций. При этом сопряженное к пространству 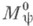 изоморфно пространству Лоренца н, следовательно, My изоморфно второму сопряженному пространству к
изоморфно пространству Лоренца н, следовательно, My изоморфно второму сопряженному пространству к 
Если
 - пространство, на s-алгебре измеримых множеств к-рого определена s-конечная мера m, то для каждой измеримой функции х(т).определена ее перестановка
- пространство, на s-алгебре измеримых множеств к-рого определена s-конечная мера m, то для каждой измеримой функции х(т).определена ее перестановка  так что можно ввести М. п. .
так что можно ввести М. п. . с нормой (1).
с нормой (1).
Лит.:[1] Marcinkiewicz J., "С. r. Acad. sci.". 1939, t. 208, p. 1272-73; [2] К р е й н С. Г., Петунин Ю. И., Семенов Е. М., Интерполяция линейных операторов, М., 1978: [3] С т е й н И., В е й с Г., Введение в гармонический анализ на евклидовых пространствах, пер. с англ., М., 1974.
С. Г. Крейн.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
