ЛИНЕЙНОЕ УРАВНЕНИЕ

алгебраическое - алгебраическое уравнение 1-й степени по совокупности неизвестных, т. е. уравнение вида

Всякая система Л. у. может быть записана в виде

где ти n - натуральные числа; а _ij (i=1, 2, . . ., т, j=1, 2, . . ., n) наз. коэффициентами при неизвестных и являются заданными; b_i (i=l, 2, . . ., т).наз. свободными членами и также являются заданными; х;(i=1, 2, . . ., n) наз. н е и з-вестными и являются искомыми. Решением системы Л. у. (1) наз. такой набор значений c₁, с ₂, . . ., с _n, что каждое из уравнений системы обращается в тождество при подстановке с _i вместо соответствующих неизвестных. Для приложений наиболее важен тот случай, когда коэффициенты при неизвестных, свободные члены и значения неизвестных являются числами (комплексными, действительными или целыми), но можно рассматривать также случай, когда они лежат в произвольном поле Р.

По числу решений системы Л. у. делятся на следующие типы:

совместная система - система Л. у., имеющая хотя бы одно решение;

несовместная система (или противоречивая) - система, не имеющая ни одного решения;

определенная система - система, имеющая единственное решение;

неопределенная система - система, имеющая более одного решения.

Если рассматриваются решения системы со значениями неизвестных в данном числовом (или любом бесконечном) поле, то каждая неопределенная система Л. у. имеет бесконечно много решений. В отличие от уравнений степени выше первой, тип системы Л. у. не меняется при расширении данного поля Р. Так, при расширении поля несовместная система не может стать совместной, а определенная - неопределенной. Однако совокупность решений неопределенной системы при этом расширяется.

Простейший путь определения типа системы (1) и вычисления ее решений дает Гаусса метод исключения неизвестных. В случае п=т система (1) тогда и только тогда является определенной, когда определитель, составленный из ее коэффициентов при неизвестных, отличен от нуля. В этом случае единственное решение системы находится по формулам Крамера (см. Крамера правило).

Для решения системы Л. у., коэффициенты к-рой содержат буквенные параметры, более удобным, чем метод Гаусса, является применение общей теории Л. у., связанной с понятием ранга матрицы. Ранг матрицы можно определить как максимальное число линейно независимых строк или столбцов. По теореме о ранге матрицы ранг системы строк матрицы равен рангу системы столбцов и равен наибольшему порядку отличных от нуля миноров этой матрицы. С системой Л. у. (1) связаны две матрицы: матрица

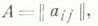
составленная из коэффициентов при неизвестных, и расширенная матрица

получаемая из матрицы Адобавлением столбца свободных членов. Критерий совместности системы (1) дает теорема Кронекера - Капелл и: система Л. у. (1) тогда и только тогда совместна, когда ранг матрицы Аравен рангу матрицы В.

Система Л. у. (1) тогда и только тогда имеет единственное решение, когда ранг матрицы Аравен рангу матрицы Ви равен п.

Неизвестные совместной системы Л. у. подразделяются на главные и свободные. При любых значениях свободных неизвестных существуют Однозначно определенные значения главных неизвестных, дающие в совокупности решение данной системы. Выбор главных и свободных неизвестных не всегда однозначен. Именно, если ранг Аравен рангу Ви равен r, то любые r неизвестных, из коэффициентов при к-рых можно составить определитель можно считать главными, а остальные - свободными. Определитель Dв этом случае наз. главным (или базисным) м и н о р о м системы. Его можно искать методом окаймления, начиная с миноров низших порядков. Он также не всегда определен однозначно. При вычислении решений надо взять лишь rуравнений, содержащих главный минор D, и выразить в общем виде (напр., используя формулы Крамера) главные неизвестные через свободные. Эти выражения наз. общим решением. Свободные неизвестные играют в нем роль свободных параметров. Придавая им любые значения, находят значения главных неизвестных, дающие вместе с выбранными значениями свободных неизвестных решение системы. Любое решение совместной системы может быть получено указанным путем при подходящих значениях свободных неизвестных. Если все коэффициенты при неизвестных и свободные члены лежат в поле Р, то при выборе для свободных неизвестных значений из того же поля Рполучается решение со значениями всех неизвестных из того же поля Р. При r=n все неизвестные являются главными и общего решения не существует. Система Л. у.

полученная из системы (1) заменой свободных членов нулями, наз. однородной системой Л. у., соответствующей системе (1). Система (2) всегда совместна (т. к. ей удовлетворяет нулевое решение). Для того чтобы она имела ненулевое решение, необходимо и достаточно, чтобы ранг ее матрицы Абыл меньше числа неизвестных п. В частности, при т=п квадратная однородная система Л. у. тогда и только тогда имеет ненулевое решение, когда ее определитель равен нулю.

Решения совместной системы Л. у. (1) и соответствующей однородной системы (2) связаны следующим образом: сумма решения системы (1) и решения системы (2) является решением системы (1); разность двух решений системы (1) - решением системы (2). Все решения системы (1) можно получить, прибавляя к каждому решению системы (2) одно и то же частное решение системы (1).

Геометрическая интерпретация решений системы Л. у. Любую строку из п элементов поля Рможно рассматривать как строку координат вектора х n -мерного векторного пространства Vнад полем Рв нек-ром фиксированном базисе. Для краткости формулировок вектор хотождествляется со строкой его координат. Все решения однородной системы (2) составляют подпространство Uпространства V. Его размерность равна n-r, где п - число неизвестных, а r - ранг матрицы Асистемы. При r<n подпространство Uотлично от нулевого и его базис наз. также фундаментальной системой решений системы Л. у. (2). Обратно, для каждого подпространства Uпространства Vсуществует однородная система Л. у., решения к-рой составляют подпространство U. Множество векторов Z= U+x₀, получаемое прибавлением к каждому вектору подпространства Uодного и того же вектора x₀, наз. линейным многообразием (или плоскостью, иногда гиперплоскостью) пространства V. Все решения совместной системы Л. у. (1) составляют нек-рое линейное многообразие Z; обратно, для любого линейного многообразия Zсуществует совместная система, решения к-рой составляют данное многообразие (см. [3]).

Решение систем линейных уравнений в целых числах. Пусть дана система уравнений (1), где все a_ij и b_i - целые числа. И пусть через обозначен наибольший общий делитель всех миноров порядка k матрицы Аиз коэффициентов при неизвестных, а через - аналогичное число для расширенной матрицы В. Если все миноры порядка kв матрице А(или В). равны нулю, то считают (соответственно ). Для того чтобы целочисленная система Л. у. (1) имела целочисленное решение, необходимо и достаточно, чтобы 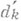нацело делилось на выполнялось равенство

Для формулировки метода вычисления всех целочисленных решений систем Л. у. вводятся т. н. элементарные преобразования целочисленных матриц: 1) прибавление к i-й строке j-й строки умноженной па целое число с;2) умножение i-й строки на -1; 3) перестановка i-й и j-й строк и аналогичные преобразования столбцов. При элементарных преобразованиях строк система (1) переходит в эквивалентную систему и, значит, совокупность целочисленных решений не меняется. При элементарных преобразованиях столбцов матрицы Аиз коэффициентов при неизвестных происходят следующие преобразования неизвестных: если - новые неизвестные, то

при преобразовании 1)

при преобразовании 2)

при преобразовании 3)

При таких преобразованиях неизвестных целочисленные решения п только они переходят в целочисленные. Систему (1), для к-рой ранг Лравен рангу Ви равен r, при помощи элементарных преобразований строк матрицы Ви столбцов матрицы А, а также отбрасыванием нулевых уравнений можно привести к следующему канонич. виду

Числа e_i удовлетворяют дополнительным условиям:

в

Для задачи решения системы в целых числах эти дополнительные условия несущественны.

Для существования целочисленных решений системы (3) необходимо и достаточно, чтобы числа

были целыми. Неизвестные у ₁, у ₂, . . ., у _r определены однозначно, а при r<n неизвестные могут принимать любые целые значения.

Для вычисления решений исходной системы (1) надо все преобразования столбцов матрицы Априменить в том же порядке к единичной матрице Епорядка п. Полученная целочисленная матрица Qдает связь старых и новых неизвестных:

где

Затем надо положить 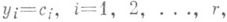а при r<n неизвестным играющим роль параметров, можно придавать любые целые значения.

Указанный метод решения системы (1) над кольцом целых чисел обобщается на любые евклидовы кольца и кольца главных идеалов.

Разыскание целочисленных решений уравнений и систем в общем случае - предмет теории диофантовых уравнений.

Лит.:[1] К у р о ш А. Г., Курс высшей алгебры, 11 изд. М., 1975: [2] К о с т р н к и н Л. И., Введение в алгебру, М. 1977; [3] Мишина А. П., Проскуряков И. В. Высшая алгебра. Линейная алгебра, многочлены, общая алгебра 2 изд.. М., 1965. И. В. Проскуряков