ЛИНЕЙНОЕ УРАВНЕНИЕ

- уравнение вида

где А- линейный оператор, действующий из векторного пространства Xв векторное пространство В, х - неизвестный элемент из X, b - заданный элемент из В(свободный член). Если 6=0, то Л. у. наз. однородным. Решением Л. у. наз. элемент обращающий (1) в тождество:

Простейший пример доставляет линейный оператор ( линейная функция )и определяемое им линейное уравнение (алгебраическое):

а, (или произвольному полю k);его решение существует тогда и только тогда, когда либо 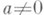(и тогда х ₀=b/а), либо а=b=0 (и тогда х ₀ - любое). Обобщением уравнения (2) является Л. у. вида

где f(х) -линейный функционал, определенный на векторном пространстве Xнад полем В частности, если размерность Xконечна и равна га (так что

Xизоморфно kⁿ), f имеет вид линейной формы нескольких переменных и уравнение (3) может быть записано в виде

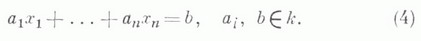
Если а _i одновременно не обращаются в нуль, то множество решений, уравнения (4) заполняет ( п-1)-мерное линейное многообразие (в однородном случае - линейное подпространство) в X. Если Xбесконечномерно, то множество решений уравнения (3) - линейное многообразие коразмерности 1.

Несколько уравнений вида (4) образуют с истому Л. у.:

При этом систему (5) можно интерпретировать как одно Л. у. вида (1), если принять в качестве Xпространство kⁿ, в качестве В - пространство k^m, а оператор Азадать матрицей Вопрос о совместности системы Л. у. (5), т. е. вопрос о существовании решения системы Л. у., решается сравнением ранга матриц

Более сложно обстоит дело в случае, когда Xн Вявляются бесконечномерными векторными пространствами. При этом играют существенную роль топологии пространств Xи Ви обусловливаемые ими те или иные свойства ограниченности, непрерывности и пр. оператора А. В общем случае существование и единственность решения Л. у. обусловлены обратимостью А(см. Обратное, отображение). Однако эффективно обратить Аудается далеко не всегда, и потому для исследования Л. у. приобретают важную роль качественные методы, позволяющие без решения Л. у. указать полезные в том или ином отношении свойства совокупности решений (в предположении, что они существуют), напр. единственность, априорные оценки и т. д. С другой стороны, оператор Аможет быть определен не на всем пространстве X, и уравнение (1) может не иметь решения ни при каких 6. В этой ситуации разрешимость уравнения (1) устанавливается (во многих практически важных случаях) выбором надлежащего расширения оператора А.

Для конкретных типов Л. у., напр. для линейных дифференциальных уравнений как обыкновенных, так и с частными производными, для линейных интегральных уравнений, разработаны специфические, в том числе и численные, методы решения и исследования. Наконец, в ряде случаев (напр., в задачах линейной регрессии) оказываются полезными значения в определенном смысле наиболее подходящие для роли решения Л. у.

М. И. Войцеховский.