ЛИ ТЕОРЕМА

- 1) Ли т. - одна из трех классич. теорем теории групп Ли, описывающих связь Ли. локальной группы с ее алгеброй Ли. Ли т. составляют фундамент теории, развитой в 19 в. С. Ли (S. Lie) и его школой (см. [1]).

Пусть G - r -мерная вещественная эффективная локальная Ли группа преобразований области е- единица группы Gи пусть в локальных координатах в окрестности множества действие группы Gна задано набором аналитич. функций

где Указанное действие определяет

на rаналитич. векторных полей

где

Первая теорема Ли устанавливает, что функции 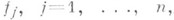определяющие действие группы G, сами определяются по нек-рому вспомогательному набору аналитич. функций на G, удовлетворяющих условию

- символ Кронекера. Точнее, - это матрица дифференциала правого сдвига на группе G на элемент g^-1 в точке g, а набор функций (1) - это в точности решение системы уравнений

удовлетворяющее начальным условиям

Вторая т е о р е м а Ли описывает свойства. функций А именно, удовлетворяют системе уравнений

(эта система есть условие интегрируемости системы (4)), а функции - в системе уравнений

где - нек-рые константы. Соотношения (5) означают, что коммутатор (скобка Ли) [X_i, X_j]векторных нолей X_i и X_j является линейной комбинацией полей с постоянными коэффициентами

т. е. что линейная оболочка полей Х ₁, ..., Х _r является алгеброй относительно скобки Ли.

Обращение первой и второй теорем Ли состоит в следующем: если функции f₁, ..., f_n дают решение системы (4), в к-рой матрица имеет максимальный ранг, и выполнены условия (3) и (5), то формула (1) определяет локальную эффективную группу Ли преобразований. Эта локальная группа порождена однопараметрич. группами преобразований, заданными формулой (2).

Третья теорема Ли утверждает, что константы удовлетворяют следующим соотношениям:

т. е. является алгеброй Ли. Важное значение имеет обращение третьей теоремы Ли: если - любые константы, удовлетворяющие соотношениям (7), то существует система векторных полей Х ₁, ..., Х _r, удовлетворяющих соотношениям (6), и эти векторные поля возникают с помощью описанной выше конструкции из нек-рой локальной группы Ли преобразований (иначе говоря, всякая конечномерная алгебра Ли есть алгебра Ли нек-рой локальной группы Ли преобразований). Иногда (см., напр., [4]) третьей теоремой Ли наз. утверждение о существовании для каждой конечномерной алгебры Ли над полем или глобальной группы Ли с алгеброй Ли (см. Ли алгебра аналитической группы).

2) Л и т. о разрешимых алгебрах Ли: пусть - линейное представление конечномерной разрешимой алгебры Ли в векторном пространстве Vнад алгебраически замкнутым полем характеристики 0; тогда в Vсуществует такой базис, в к-ром все операторы Xиз записываются верхнетреугольными матрицами. Аналогичное утверждение справедливо и для линейного непрерывного представления связной топологической разрешимой группы в конечномерном комплексном векторном пространстве (теоретико-групповой аналог Ли т.); предположение о связности группы является существенным. Вариант теоретико-группового аналога Ли т. известен под названием Ли - Колчина теорема.

Лит.:[1] L i е S., Е n g е l F., Theorie der Transformationsgruppen, Bd 1-3, Lpz., 1888-93; [2] Бурбаки Н., Группы и алгебры Ли. Алгебры Ли, свободные алгебры Ли и группы Ли, пер. с франц., М., 1976; [3] Л о н т р я г и н Л. С., Непрерывные группы, 3 изд., М., 1973; [4] С е р р Ж. -П., Алгебры Ли и группы Ли, пер. с англ. и франц., М., 1969; [6] Шевалле К., Теория групп Ли, пер. с франц., т. 3, М., 1958; [5] Чеботарев Н. Г., Теория групп Ли, М.-Л., 1940. В. Л. Попов.