ЛИ АЛГЕБРАИЧЕСКАЯ АЛГЕБРА
- ЛИ АЛГЕБРАИЧЕСКАЯ АЛГЕБРА
- 1) Алгебра Ли алгебраич. подгруппы (см. Алгебраическая группа).полной линейной группы, всех автоморфизмов конечномерного векторного пространства Vнад полем k. Если 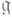 - произвольная подалгебра в алгебре Ли всех эндоморфизмов V, то существует наименьшая Ли а. а., содержащая
- произвольная подалгебра в алгебре Ли всех эндоморфизмов V, то существует наименьшая Ли а. а., содержащая  она наз. алгебраической оболочкой подалгебры Ли
она наз. алгебраической оболочкой подалгебры Ли  Для алгебраичности алгебры Лн
Для алгебраичности алгебры Лн  над произвольным алгебраически замкнутым полем kнеобходимо, чтобы вместе с каждым линейным оператором
над произвольным алгебраически замкнутым полем kнеобходимо, чтобы вместе с каждым линейным оператором  в
в  лежали его полупростая и нильпотентная компоненты sи п(см. Жордана разложение). Это условие определяет т. н. почти алгебраические алгебры Ли. Оно не является достаточным для того, чтобы
лежали его полупростая и нильпотентная компоненты sи п(см. Жордана разложение). Это условие определяет т. н. почти алгебраические алгебры Ли. Оно не является достаточным для того, чтобы 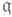 была Ли а. а. В случае поля kхарактеристики 0 необходимое и достаточное условие алгебраичности алгебры Ли
была Ли а. а. В случае поля kхарактеристики 0 необходимое и достаточное условие алгебраичности алгебры Ли  состоит в том, что вместе с га и
состоит в том, что вместе с га и 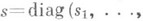
 в
в  лежат все операторы вида
лежат все операторы вида 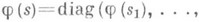
 где
где  - произвольное
- произвольное 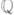 -линейное отображение из kв k. Исследовано [3] строение Ли а. а. в случае поля характеристики р> 0.
-линейное отображение из kв k. Исследовано [3] строение Ли а. а. в случае поля характеристики р> 0.
2) Алгебра Ли Lнад коммутативным кольцом k, в к-рой для любого элемента 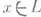 -эндоморфизм
-эндоморфизм 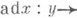
 заданный на L, является корнем нек-рого многочлена со старшим коэффициентом 1 и остальными коэффициентами из k. Конечномерная над полем kалгебра Ли является Ли а. а. Обратное неверно: над любым полем kсуществуют бесконечномерные Ли а. а. с конечным числом порождающих [4]. Ряд вопросов о Ли а. а. получает решение уже в классе Ли нильалгебр.
заданный на L, является корнем нек-рого многочлена со старшим коэффициентом 1 и остальными коэффициентами из k. Конечномерная над полем kалгебра Ли является Ли а. а. Обратное неверно: над любым полем kсуществуют бесконечномерные Ли а. а. с конечным числом порождающих [4]. Ряд вопросов о Ли а. а. получает решение уже в классе Ли нильалгебр.
Лит.:[1] Б о р е л ь А., Линейные алгебраические группы, пер. с англ., М., 1972; [2] Ш е в а л л е К., Теория групп Ли, пер. с франц., т. 2, М., 1958; [3] S е 1 i g m a n G., Modular Lie algebras, В.- Hdlb.- N. Y., 1967; [4] Голод Е. С., "Изв. АН СССР. Сер. матем.", 1964, т. 28, № 2, с. 273-76.
Ю. А. Бахтурин.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ЛИ АЛГЕБРАИЧЕСКАЯ АЛГЕБРА" в других словарях:
АЛГЕБРАИЧЕСКАЯ АЛГЕБРА — алгебра А с ассоциативными степенями (в частности, ассоциативная) над полем F, все элементы к рой являются алгебраическими (элемент наз. алгебраическим, если порожденная им подалгебра F[a]конечномерна, или, что равносильно, элемент аобладает… … Математическая энциклопедия
Алгебраическая система — (или алгебраическая структура) в универсальной алгебре множество (носитель) с заданным на нём набором операций и отношений (сигнатура), удовлетворяющим некоторой системе аксиом. Алгебраическая система с пустым множеством отношений… … Википедия
АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия
Алгебра (значения) — Алгебра раздел математики либо математическая структура специального вида (см. Алгебраическая система) Как раздел математики Абстрактная алгебра Алгебра логики раздел математической логики. Коммутативная алгебра Линейная алгебра… … Википедия
Алгебра кортежей — Алгебра кортежей математическая система моделирования и анализа многоместных отношений. Содержание 1 Использование термина 2 Определение 3 На чем … Википедия
Алгебра Хопфа — Алгебра Хопфа алгебра, являющаяся унитарной ассоциативной коалгеброй и, таким образом, биалгеброй c антигомоморфизмом специального вида. Названа в честь Х. Хопфа. Алгебры Хопфа встречаются в алгебраической топологии, где они возникли в… … Википедия
Алгебраическая геометрия — Алгебраическая геометрия раздел математики, который объединяет абстрактную алгебру с геометрией. Главным предметом изучения классической алгебраической геометрии, а также в широком смысле и современной алгебраической геометрии, являются… … Википедия
Алгебраическая геометрия над алгебраическими системами — (другое название универсальная алгебраическая геометрия[1]) раздел математики, изучающий связи между элементами алгебраической системы, которые варажаются на языке алгебраических уравнений над алгебраическими системами. Классическая… … Википедия
Алгебра Клини — в теоретической информатике, специальная алгебраическая структура, введённая американским математиком Стивеном Клини, являющаяся обобщением алгебры регулярных выражений. Определение Алгеброй Клини называется алгебра сигнатуры , являющаяся… … Википедия
Алгебраическая функция — Алгебраическая функция элементарная функция, которая в окрестности каждой точки области определения может быть неявно задана с помощью алгебраического уравнения. Формальное определение: Функция называется алгебраической в точке , если… … Википедия
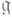 - произвольная подалгебра в алгебре Ли всех эндоморфизмов V, то существует наименьшая Ли а. а., содержащая
- произвольная подалгебра в алгебре Ли всех эндоморфизмов V, то существует наименьшая Ли а. а., содержащая  она наз. алгебраической оболочкой подалгебры Ли
она наз. алгебраической оболочкой подалгебры Ли  Для алгебраичности алгебры Лн
Для алгебраичности алгебры Лн  над произвольным алгебраически замкнутым полем kнеобходимо, чтобы вместе с каждым линейным оператором
над произвольным алгебраически замкнутым полем kнеобходимо, чтобы вместе с каждым линейным оператором  в
в  лежали его полупростая и нильпотентная компоненты sи п(см. Жордана разложение). Это условие определяет т. н. почти алгебраические алгебры Ли. Оно не является достаточным для того, чтобы
лежали его полупростая и нильпотентная компоненты sи п(см. Жордана разложение). Это условие определяет т. н. почти алгебраические алгебры Ли. Оно не является достаточным для того, чтобы 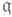 была Ли а. а. В случае поля kхарактеристики 0 необходимое и достаточное условие алгебраичности алгебры Ли
была Ли а. а. В случае поля kхарактеристики 0 необходимое и достаточное условие алгебраичности алгебры Ли  состоит в том, что вместе с га и
состоит в том, что вместе с га и 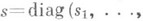
 в
в  лежат все операторы вида
лежат все операторы вида 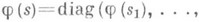
 где
где  - произвольное
- произвольное 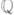 -линейное отображение из kв k. Исследовано [3] строение Ли а. а. в случае поля характеристики р> 0.
-линейное отображение из kв k. Исследовано [3] строение Ли а. а. в случае поля характеристики р> 0.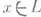 -эндоморфизм
-эндоморфизм 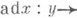
 заданный на L, является корнем нек-рого многочлена со старшим коэффициентом 1 и остальными коэффициентами из k. Конечномерная над полем kалгебра Ли является Ли а. а. Обратное неверно: над любым полем kсуществуют бесконечномерные Ли а. а. с конечным числом порождающих [4]. Ряд вопросов о Ли а. а. получает решение уже в классе Ли нильалгебр.
заданный на L, является корнем нек-рого многочлена со старшим коэффициентом 1 и остальными коэффициентами из k. Конечномерная над полем kалгебра Ли является Ли а. а. Обратное неверно: над любым полем kсуществуют бесконечномерные Ли а. а. с конечным числом порождающих [4]. Ряд вопросов о Ли а. а. получает решение уже в классе Ли нильалгебр.