ЛЕВИ - ХИНЧИНА КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ

- формула для логарифма характеристич. функции 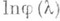безгранично делимого распределения:

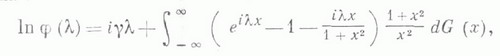
где подинтегральная функция при x=0 равна - l²/2 и характеристики Л.- X. к. п. g и Gудовлетворяют следующим условиям: g - действительное число, G(x).- неубывающая непрерывная слева функция ограниченной вариации.

Л.-X. к. п. было предложено А. Я. Хинчиным (1937) и эквивалентно формуле, предложенной несколько ранее П. Леви (P. Levy, 1934) и называемой Леви каноническим представлением. Каждому безгранично делимому распределению соответствует единственный набор характеристик Л.- X. к. п. g и G, и обратно, при условиях на g и G, приведенных выше, по любому такому набору Л.- X. к. п. определяет логарифм характеристич. функции нек-рого безгранично делимого распределения. Для слабой сходимости последовательности безгранично делимых распределений, определяемых характеристиками g_n, G_n, n=1, 2, . . ., к распределению (которое необходимо будет безгранично делимым) с характеристиками g и G необходимо и достаточно, чтобы вполне сходились к G при

Лит. см. при ст. Леви каноническое представление.

Б. А. Рогозин.