- КУБИЧЕСКАЯ ФОРМА
однородный многочлен третьей степени от нескольких переменных с коэффициентами из нек-рого фиксированного поля или кольца. Пусть k - нек-рое поле и F3(x0,. . . , х п )-К. ф. с коэффициентами из k(говорят, что это - К. ф. над k}. Уравнение
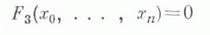
определяет кубическую гиперповерхность в проективном пространстве Р n, что сводит алгебро-геометрическую теорию К. ф. над алгебраически замкнутым полем kк теории кубических гиперповерхностей (см. [1]).
Арифметич. теория К. ф. над числовыми полями (и их кольцами целых) развита пока (1982) недостаточно полно по сравнению с богатой и содержательной арифметич. теорией квадратичных форм. Для К. ф. от двух переменных арифметич. теория - это теория кубич. расширений числовых полей (см. [2]). Для К. ф. от трех переменных арифметич. теория - это часть арифметич. теории эллиптич. кривых (см. [3]). В частности, для К. ф. от трех переменных известны примеры нарушения принципа Хассе. Для К. ф. от четырех переменных (см. [1, 4, 6]) также известны примеры нарушения принципа Хассе. Для К. ф. от большего числа переменных нет никакой общей теории.
В чисто алгебраич. теории К. ф. кроме результатов о структуре множеств точек на кубич. гиперповерхностях имеется еще ряд результатов классич. теории инвариантов. А именно, известно строение алгебры (абсолютных) инвариантов К. ф. от двух и трех переменных; в этих случаях она не имеет сизигий и является алгеброй многочленов соответственно от одного (степени 4) и двух (степени 4 и 6) алгебраич. независимых однородных образующих. Если число переменных больше трех, указанная алгебра имеет сизигии [5] и устроена весьма сложно. Орбиты, их стабилизаторы и канонич. представители, а также семейства орбит относительно естественного действия группы
 на пространстве всех К. ф. от трех и четырех переменных изучались А. Пуанкаре [6].
на пространстве всех К. ф. от трех и четырех переменных изучались А. Пуанкаре [6].
Лит.:[1] Манин Ю. И., Кубические формы. Алгебра, геометрия, арифметика, М., 1972; [2] Д е л о н е В. Н., Фаддеев Д. К., Теория иррациональностей третьей степени, М.-Л., 1940 (Тр. Матем. ин-та АН СССР, т. И); [3] Касселс Д ж., "Математика", 1968, т. 12, № 1, с. 113-60; .№ 2, с. 3-48; [4] S е g r е В., "Math. Notae", [Univ. Rosario], 1951, v. 11, p. 1-68; [5] К а ц В. Г., П о п о в В. Л., Винберг Е. Б., "С. r. Acad. sci.", 1976, t. 283, p. 875-78; [6] II у а н к а р е А., Избр. труды, пер. с франц., т. 2, М., 1972, с. 819-900. В. А. Псковских, В. Л. Попов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
