- КОЭНА - МАКОЛЕЯ КОЛЬЦО
маколеево к о л ь ц о, - коммутативное локальное нётерово кольцо А, глубина prof Aк-poro равна его размерности dim А. Гомологич. характеризация К.- М. к. Асостоит в том, что группы
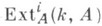 или группы локальных когомологий
или группы локальных когомологий  обращаются в нуль при всех
обращаются в нуль при всех 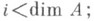 здесь m - максимальный идеал, a k- поле вычетов А. Можно дать определение К.-М. к., используя понятие регулярной последовательности. Так называется последовательность
здесь m - максимальный идеал, a k- поле вычетов А. Можно дать определение К.-М. к., используя понятие регулярной последовательности. Так называется последовательность  элементов m такая, что для всех iэлемент а i не делит нуль в
элементов m такая, что для всех iэлемент а i не делит нуль в  Локальное кольцо Аназ. К.- М. к., если существует регулярная последовательность
Локальное кольцо Аназ. К.- М. к., если существует регулярная последовательность  для к-рой факторкольцо артиново. В этом случае
для к-рой факторкольцо артиново. В этом случае 

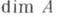
Если
 - простой идеал в К.- М. К. А , то для его высоты
- простой идеал в К.- М. К. А , то для его высоты 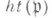 (см. Высота идеала).выполняется соотношение
(см. Высота идеала).выполняется соотношение

В частности, К.- М. к. равноразмерное и цепное. Фундаментальным результатом о К. -М. к. является следующая теорема о несмешанности. Пусть Аесть d-мерное К.- М. к., а %, . . ., ak - последовательность элементов Аи
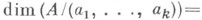
 Тогда последовательность а 1( . . ., ak регулярна, и идеал
Тогда последовательность а 1( . . ., ak регулярна, и идеал 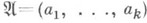 несмешанный, т. е. любой простой идеал, ассоциированный с
несмешанный, т. е. любой простой идеал, ассоциированный с  имеет высоту kи ковысоту d-k. Теорема о несмешанности была доказана Ф. Маколеем [1] для кольца многочленов и И. Коэном [2] для кольца формальных степенных рядов.
имеет высоту kи ковысоту d-k. Теорема о несмешанности была доказана Ф. Маколеем [1] для кольца многочленов и И. Коэном [2] для кольца формальных степенных рядов.
Примеры К.- М. к. Регулярное локальное кольцо (и, вообще, любое кольцо Горенштейна) является К.- М. к.; любое артиново кольцо, любое одномерное приведенное кольцо, любое двумерное нормальное кольцо являются К.- М. к. Если А - локальное К.- М. к., то такими же будут его пополнение, кольцо формальных степенных рядов над Аи любое конечное плоское расширение. К.- М. к. будет и полное пересечение в К.- М. к. А, т. е. факторкольцо вида
 где последовательность в], - . ., а k регулярна. Наконец, локализация К.- М. к. в простом идеале снова является К.- М. к. Ото позволяет расширить определение К.- М. к. на произвольные кольца и схемы. А именно, нётерово кольцо А(схема X).наз. кольцом Коэна - Маколея (схемой Коэна - Маколея), если для любого простого идеала
где последовательность в], - . ., а k регулярна. Наконец, локализация К.- М. к. в простом идеале снова является К.- М. к. Ото позволяет расширить определение К.- М. к. на произвольные кольца и схемы. А именно, нётерово кольцо А(схема X).наз. кольцом Коэна - Маколея (схемой Коэна - Маколея), если для любого простого идеала  (соответственно любой точки
(соответственно любой точки 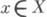 ) локальное кольцо
) локальное кольцо  (соответственно
(соответственно  ) является К.- М. к. В этом более широком смысле К.- М. к. является кольцо многочленов над полем и даже над любым К.- М. к., а также полугрупповое кольцо
) является К.- М. к. В этом более широком смысле К.- М. к. является кольцо многочленов над полем и даже над любым К.- М. к., а также полугрупповое кольцо  где G - выпуклый многогранный конус в
где G - выпуклый многогранный конус в 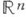 (см. [6]).
(см. [6]).
К.- М. к. стабильны и при переходе к кольцам инвариантов. Если G - конечная группа, действующая на К.- М. к. А, причем ее порядок обратим в Л, то кольцо инвариантов А G также есть К.- М. к.
Для градуированного кольца Асвойство быть К.- М. к. проявляется в когомологиях обратимых пучков на проективной схеме
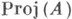 (см. [4]). Если однородное кольцо Аконуса в А n+1, связанного с проективным многообразием
(см. [4]). Если однородное кольцо Аконуса в А n+1, связанного с проективным многообразием 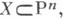 является К.- М. к., то Xназ. арифметическим многообразием Коэна - Маколея. В этом случае кольцо Аизоморфно
является К.- М. к., то Xназ. арифметическим многообразием Коэна - Маколея. В этом случае кольцо Аизоморфно  для всех
для всех 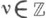 и для
и для 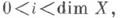 где
где  есть v-я тензорная степень поляризующего обратимого пучка
есть v-я тензорная степень поляризующего обратимого пучка  на X. Этим свойством обладают проективные пространства и их произведения, полные пересечения, многообразия Грассмана и подмногообразия Шуберта [7], многообразие флагов и обобщенное многообразие флагов [8].
на X. Этим свойством обладают проективные пространства и их произведения, полные пересечения, многообразия Грассмана и подмногообразия Шуберта [7], многообразие флагов и обобщенное многообразие флагов [8].
Модуль Мнад локальным кольцом Аназ. модулем Коэна - Маколея, если его глубина равна размерности. На модули Коэна - Маколея распространяются многие результаты о К.- М. к.; напр., носитель такого модуля равноразмерен. Существует гипотеза, что любое полное локальное кольцо обладает модулем Коэна - Маколея Мтаким, что dim M=dim A.
Лит.:[1] Macaulay P. S., The algebraic theory of modular systems, Camb., 1916; [2] С о h e n I. S., "Trans. Amer. Math. Soc.", 1946, v. 59, p. 54-106; [3] 3 a p и с с к и и (3., Самюэль П., Коммутативная алгебра, пер-, с англ., т. 2, М., 1963; [Л] М а м ф о р д Д., Лекции о кривых на алгебраической поверхности, пер. с англ., М., 1968; [5] С е р р Ж.-П., "Математика", 1963, т. 7, № 5, с. 3-93; [6] Н о с h s t е г М., "Ann. Math.", 1972, v. 96, p. 318-37; [7] е г о же, "J. Algebra", 1973, v. 25, р. 40-57; [8] К е m р t G.R., "Ann. Math.", 1976, v. 103, p. 557 - 91. B. И. Данилов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
