КОНТИНУУМ-ГИПОТЕЗА

- гипотеза Г. Кантора (G. Cantor, 1878), состоящая в том, что всякое бесконечное подмножество континуума R равномощно либо множеству натуральных чисел, либо R. Эквивалентная формулировка (при наличии выбора аксиомы):

(см. Алефы). Обобщение этого равенства на произвольные кардинальные числа наз. обобщенной континуум-гипотезой: для всякого ординального числа a

В отсутствии аксиомы выбора обобщенная К.-г. формулируется в виде

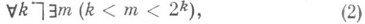
где k, т.- переменные для бесконечных кардинальных чисел. Из (2) вытекают аксиома выбора и (1), а из (1) и аксиомы выбора вытекает (2).

Д. Гильберт (D. Hilbert) в своем знаменитом списке проблем поставил под номером 1 проблему доказать гипотезу континуума Кантора (проблема континуума). В рамках традиционного теоретико-множественного решения проблема не поддавалась решению. Среди математиков росло убеждение в принципиальной неразрешимости проблемы континуума. Лишь после того, как был найден способ сведения математич. понятий к теоретико-множественным, выявлены аксиомы, сформулированные на теоретико-множественном языке, к-рые можно положить в основу реально встречающихся математич. доказательств, и формализованы логич. средства вывода, стало возможным точно поставить, а затем и решить вопрос о формальной неразрешимости К.-г. Формальная неразрешимость понимается в смысле не существования формального вывода в системе Цермело - Френкеля ZF как для К.-г., так и для ее отрицания.

В 1939 К. Гёдель (К. Godel) установил недоказуемость отрицания обобщенной К.-г. (а следовательно, н недоказуемость отрицания К.-г.) в системе ZF с аксиомой выбора (системе ZFC), в предположении, что ZF непротиворечива (см. Конструктивное по Гёделю множество). В 1963 П. Коэн (P. Cohen) показал невыводимость К.-г. (а следовательно, и невыводимость обобщенной К.-г.) из аксиом ZFC при условии непротиворечивости ZF (см. Вынуждения метод).

Являются ли эти результаты окончательными в проблеме континуума? Ответ на этот вопрос зависит от отношения к посылке о непротиворечивости ZF и, что . более существенно, к тому экспериментальному факту, что всякое содержательное математич. доказательство (традиционной классич. математики), после того как оно найдено, может быть адекватным образом формализовано в системе ZFC. Факт этот нельзя не только доказать, но даже точно сформулировать, поскольку всякое уточнение поднимает аналогичный вопрос об адекватности уточнения уточняемому.

На теоретико-модельном языке К. Гёдель и П. Коэн построили модели для ZFC, в к-рых

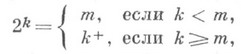
где т- произвольный, наперед заданный несчетный регулярный кардинал, а k⁺- первое кардинальное число, большее к. Каково возможное поведение функции 2^k в различных моделях ZFC?

Известно, что на регулярных кардиналах kфункция эта может вести себя как угодно, подчиняясь лишь условиям

где cf (т) - наименьший кардинал конфинальный т(см. кардинальное число). Для сингулярных (т. е. не регулярных) кзначение функции 2^k может зависеть от ее поведения на меньших кардинальных числах. Так, напр., если равенство (1) пмеет место для всех a<w₁, то оно имеет место и для a=w₁.

Лит.:[1] Коэн П. Дж ., Теория множеств и континуум-гипотеза, пер. с англ., М., 1969; [2] Ваumgаrtnеr J. Е., Prikry K.,"Amer. Math. Monthly", 1977, v. 84, № 2, p. 108- 113.

В. Н. Гришин.