- КОНТИНУУМ
- непустое связное хаусдорфово бикомпактное пространство. К. наз. вырожденным, если он состоит из одной точки. Особо важным является класс метризуемых К. Примеры К.: замкнутый отрезок, окружность, выпуклый многогранник и т. д. Компакт (X, р) (т. е. метризуемый бикомпакт с метрикой р) есть К. в том и только в том случае, если для каждой пары точек
и для любого e>0 найдется конечная е-цепь, соединяющая эти точки, т. е. последовательность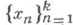 
точек в Xтакая, что х 1= а, х k=b и р( х п, xn+1)<e. Объединение двух К., имеющих общую точку, есть К. Топологич. произведение К. есть К., непрерывный образ К. есть К., компоненты бикомпакта суть К., пересечение убывающей последовательности К. есть К. Никакой К. нельзя разложить в объединение счетного семейства непересекающихся замкнутых множеств (теорема Серпиньского).Каждый локально связный метрич. К. является непрерывным образом замкнутого отрезка (теорема Хана - Мазуркевича). Невырожденный К. неприводим между двумя своими точками, если никакой его собственный подконтинуум не содержит этих двух точек К., неприводимый между некоторыми двумя своими точками, наз. неприводимым континуумом. Всякий локально связный неприводимый К. есть простая дуга, т. о. гомеоморфен отрезку.
Невырожденный К. наз. неразложимым, если его нельзя представить в виде суммы двух собственных подконтинуумов, и - наследственно неразложимым, если неразложим он сам, и неразложимы все его подконтинуумы. К. неразложим тогда и только тогда, когда в нем существуют три такие точки, что он неприводим между любыми двумя из них; все наследственно неразложимые К. гомеоморфны между собой.
Лит.:[1] Куратовский К., Топология, пер. с англ., т. 2, М., 1969.
П. С. Александров, Л. Г. Замбахидзе.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
