КАРТОГРАФИИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ

- задачи, возникающие при построении математич. основы географических и специальных карт, именно, при разработке теории картографических проекций, исследовании их свойств, преобразований, методов изысканий и др. Поверхность Земли при этом принимают либо за сферу, либо за эллипсоид вращения.

Основным объектом изучения в математич. картографии является картографич. проекция: отображение на плоскости всей поверхности земного эллипсоида (шара) или какой-либо ее части:

где и- широта, v- долгота точки (Д - односвязная область эллипсоида); х, у определяют на плоскости точку Q- изображение точки D- область изображения Д. Функции f₁ и f₂ удовлетворяют следующим условиям: они однозначные, дважды непрерывно дифференцируемые, имеют якобиан h= д( х, у)/д( и, v)0 (для сохраняющих ориентацию отображений, используемых в геодезии и картографии, h>0). Большинство фактов математич. картографии относится не только к отображениям эллипсоида на плоскость, но и к отображениям произвольных поверх-

ностей, поэтому далее под картография, проекцией (1) понимается отображение на где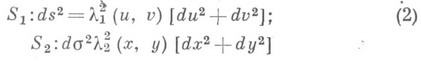

- любые регулярные поверхности; D и D- односвязные области. Выбор для целей отображения таких координат, кроме простоты записи в них линейного элемента поверхности и выгоды их использования при последующих вычислениях, обусловлен еще и тем, что переход к ним от произвольных криволинейных координат на поверхности непосредственно доставляет конформное отображение поверхности на плоскость (см. [6], [3]). Эти координаты даже на произвольной поверхности наз. иногда картографическими координатами (см. [9]); в геодезии и картографии их наз. изометрическими координатами.

Знание уравнений (1) отображения S₁ на S₂ позволяет изучить метрич. свойства отображения (см. [7], [2]), т. е. найти его характеристики: масштаб отображения m=ds/ds, причем m= m(u, v;a), и, в частности, масштабы по направлениям координатных линий m=m|_v=const, n=m|_{u = const}

поворот y изображения в направлении линии ии его поворот cв направлении линии v:

угол q между образами параметрич. линий:

искажение этого угла:

масштаб площади:

наибольшее искажение углов:

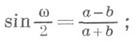
и др. Большое значение имеют главные масштабы a=m_max и b=e_min, связанные с т, п,q теоремами Аполлония:

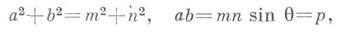
и соответствующие им главные направления, ортогональные как на S₁ (tg 2a₀=2f/(e-g), где

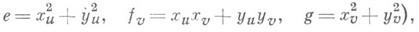
так и на S₂ С указанной сетью Тиссо на S₂ связывается индикатриса отображения - эллипс искажений {а, b, А ₀, y}, трактуемый в касательной плоскости к S₂ в точке Qкак эллипс, подобный и подобно расположенный тому бесконечно малому эллипсу (главной части отображения), к-рый является - с точностью до о(r) - изображением окружности бесконечно малого радиуса р, взятой в касательной плоскости к S₁ в точке Р. Из приведенных характеристик, выраженных через коэффициенты первых квадратичных форм взаимно отображаемых поверхностей (2) и частные производные 1-го порядка отображающих функций (1), независимы только четыре. Выбор групп независимых характеристик неоднозначен, и вместо {а, b, А ₀,y)} часто берут {т, п,y, q}.

По характеру искажений среди картографич. проекций выделяют следующие проекции: а) конформные, или равноугольные ( т=п,9=p/2); б) эквивалентные, или равновеликие (р= 1); в) эквидистантные, или равнопромежуточные (а=1, или b=1); г) геодезические, в картографии наз. ортодромическими (ортодрома - геодезическая на сфере), при к-рых геодезические на S₁ переходят в геодезические на S₂;и др. Построение проекций, обладающих объединением хотя бы двух из перечисленных свойств а) - г), возможно только при отображении поверхности на изометричные ей поверхности и в нек-рых других тривиальных случаях. Так как условия конформности и эквивалентности для целей картографии не совместимы, то для нее особое значение имеют проекции эквидистантные, к-рые по характеру искажений занимают промежуточное место между отображениями а) и б). Выделение отдельных совокупностей картографич. проекций делают обычно указанием присущих им свойств, напр. вида а) - в), т. е. заданием их уравнениями в характеристиках, к-рые с учетом формул теории искажений легко преобразуются в уравнения с частными производными 1-го порядка. Множество решений конкретной системы двух таких уравнений описывает определенный класс проекций. По типу этих уравнений проекциям приписывают соответствующий тип (эллиптический, гиперболический и т. д.).

Использование в картографии приведенных выше формул теории искажений позволяет выполнить выбор нужной для конкретной цели проекции: установив каким-либо образом уравнения проекции (1) (напр., задав на плоскости общий вид изображения координатных линий эллипсоида и, возможно, использовав при этом нек-рые дополнительные условия - конформности, эквивалентности и др.), можно на основании этих формул исследовать отображение и, варьируя его параметрами, подобрать наиболее подходящую проекцию для картографирования заданной Кроме такого решения прямой задачи, в ней используются и иные методы (геометрические, графоаналитические и др.). В обратных задачах картографии проекции изыскивают на основе априорного задания искажений в них (см. [11]). При этом первоочередное значение имеет вопрос существования требуемых проекций. Ответ на этот вопрос дает основная система уравнений в теории отображения поверхностей (см. [4]):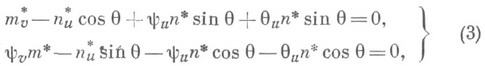

в к-рой

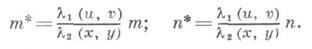
При отображении поверхности на плоскость: l₂( х, у)=1, при отображении плоских областей друг на друга также и l₁(u, v)=1. Система (3)- недоопределенная: двумя ее уравнениями связаны четыре независимые характеристики отображения; различные способы доопределения и интерпретации системы дают возможности разнообразным ее приложениям. Система (3) - квазилинейная относительно любой пары характеристик. Имеют место следующие теоремы.

Теорема 1. Характеристики m, п,y, q отображения области на область осуществляемого однозначными дважды непрерывно дифференцируемыми функциями (1) с якобианом, сохраняющим знак в области Д, удовлетворяют во всех точках этой области системе (3).

Теорема 2. Пусть выделена односвязная область D данной регулярной поверхности и пусть в области D заданы четыре функции j_i=j_i(u, v), непрерывные в D вместе со своими частными производными 1-го порядка и принимающие значения из любой односвязной области П, принадлежащей 4-мерному параллелепипеду

Если эти функции принять за характеристики нек-рого отображения на плоскость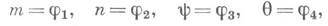

и если они удовлетворяют в D системе (3), то восстанавливаемое по ним отображение на нек-рую область D" плоскости хОу гомеоморфно, дважды непрерывно дифференцируемо, имеет в D якобиан h>0 и переводит любую точку 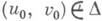в заданную точку ( х ₀, у ₀ )плоскости ху.

Теорема 2 дает при заданном распределении характеристик условия существования отображений односвязной области D поверхности S_l на нек-рую область Dплоскости S₂ при соответствии одной внутренней точки (u₀, v₀ )своему изображению ( х ₀, у ₀ )на плоскости; граница области Dпри этом неизвестна. Незнание области изображения характерно для К. м. з.: она либо определяется после установления отображающих функций (1), либо должна быть найдена на основе дополнительных условий, напр, условий минимизации искажений в проекции.

При отображениях сферы на плоскость система (3) переходит в так наз. систему Эйлера - Урмаева (см. [5], [11]), а при отображениях плоских областей, когда система (3) доопределена записанной в характеристиках системой уравнений отображения, она дает как следствие производную систему квазиконформных отображений (см. [12]). Сведение отображений поверхностей к квазиконформным отображениям плоских областей (с ограниченным искажением) вполне естественно, и первые, т. е. отображения (1) заданной области на заданную область , могут интерпретироваться как "тройная" проекция: область конформно отображается на область А плоскости uv, область конформно отображается на область Dплоскости хОу, область А плоскости uOv квазиконформно преобразуется в область Dплоскости 'хОу. Квазиконформное отображение плоских областей 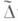на 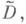сопутствующее отображению на имеет следующие характеристики: V=m*,a=y, W=n*sin 0, угол q имеет тот же смысл, что и выше. Связь рассматриваемых изображений дала возможность (см. [4]) использовать в К. м. з. теорию квазиконформных отображении плоских областей. При этом систему уравнений любого класса картографич. проекций или, более общо, всякую нелинейную систему дифференциальных уравнений вида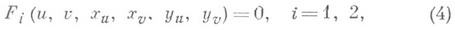

после ее записи в характеристиках

удается редуцировать к квазилинейной системе, к-рая следует из системы (3) после ее доопределения системой (5) и к-рая трактуется как производная система исходной системы (4). При этом, однако, остается открытым вопрос о соотношении типов этих двух систем: исходной и производной.

Аппарат квазиконформных отображений плоских областей (с двумя парами характеристик) может быть привлечен также в качестве теоретич. основы приборного (с использованием механич.. оптич., электронных и других устройств) преобразования картографич. проекций, точнее, преобразования двух заданных односвязных плоских областей друг в друга, каждая из к-рых является результатом картографирования одной и той же области земного эллипсоида, но в различных проекциях.

Одной из основных задач картографии (в области создания мелкомасштабных и частично среднемасштабных карт) является проблема наивыгоднейших картографич. проекций, т. е. таких отображений заданной области Л поверхности Sна плоскость, в к-рых искажения (в нек-ром заранее оговоренном смысле) сведены к минимуму (см. [2]). Наиболее распространенными критериями достоинств картографич. проекций являются следующие:

критерий Эйри:

критерий Иордана:

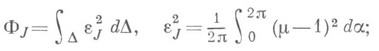
критерий Эйри - Каврайского:

критерий Иордана - Каврайского:

причем все они суть вариационного типа, и

критерий Чебышева - критерий минимаксного типа, согласно к-рому качества проекции оцениваются либо величиной

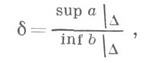
либо ее логарифмом, либо просто максимумом модуля логарифма масштаба в пределах отображаемой территории. В соответствии с тем, критерий какого вида используется при построении проекции, различают выгоднейшие проекции вариационного и минимаксного типов. Таким образом, проблемы построения наивыгоднейших проекций заключаются в том, что для заданной односвязной области D поверхности Sтребуется отыскать (при условии минимума одного из приведенных функционалов Ф или величины б) проекцию D на плоскость либо из всего их множества (1) - такие проекции наз. идеальными, либо из какой-либо их совокупности (напр., из класса проекций, описываемых решениями соответствующей ему системы (4)) - такие проекции наз. наилучшими проекциями данной их совокупности (класса). Для каждой такой задачи должна быть исследована корректность ее постановки.

Для сферич. сегмента (области сферы, ограниченной окружностью малого круга) в соответствии с критерием Чебышева идеальной проекцией (см. [2], [13]) является равнопромежуточная проекция Постеля; наилучшей конформной - стереографическая (см. [8]); наилучшей эквивалентной - равновеликая проекция Ламберта (см. [2]). На основании вариационного критерия для сферич. сегмента Эйри (см. [14]) была вычислена наилучшая азимутальная проекция. Для сферич. трапеции - области сферы, ограниченной дугами двух меридианов и двух параллелей, и (в некотором смысле) близких к ней областей при картографировании используют конические проекции.

Среди этих проекций, предназначенных для картографирования сферич. трапеций, известны наилучшие проекции минимаксного типа (проекции Маркова, см. [10]), а также наилучшие (того же типа) конформные и эквивалентные (см. [2]). Разработана общая методика построения наилучших по критерию Эйри конич. проекций (конформных, эквивалентных, равнопромежуточных) для односвязных областей произвольных очертаний (см. [15], [2]). Однако для сферич. трапеции при изображении ее на плоскости в конформной проекции наименьшее колебание логарифма масштаба имеет место в проекциях, рассчитанных (см. [9], [И]) в соответствии с теоремой Чебышева - Граве (см. [8], [9]): для того чтобы в конформной проекции (m=n, e=0) на плоскость одндсвязной области D поверхности S, имеющей полную кривизну одного и того же знака, логарифм масштаба наименее уклонялся от нуля, необходимо и достаточно постоянство масштаба на контуре изображаемой территории. Конформные проекции, удовлетворяющие условиям этой теоремы, наз. чебышевскими проекциями. Они обладают рядом полезных свойств (в них Ф _J-K = min, минимальна средняя кривизна изображений геодезич. линий поверхности S, maxD|ln p|=min), за счет к-рых они ценны для практики. П. Л. Чебышев решил задачу отыскания для конформной проекции с минимумом искажения площадей, т. е. конформной проекции, наиболее близкой к эквивалентным.

Важна и обратная задача: среди всех эквивалентных проекций области на плоскость найти проекцию с минимумом искажений форм. Один из подходов к этой задаче таков. Ввиду разной мощности двух рассматриваемых множеств проекций (множество конформных описывается системой двух уравнений с частными производными m=n, e=0, а эквивалентных - одним р=тпcos e-1) сначала из совокупности эквивалентных проекций выделяется нек-рый класс проекций, близких к конформным, а затем уже в нем ищется проекция с минимумом искажений форм. Из классич. наследия был известен один класс таких проекций, именно, класс эйлеровых проекций: р=1,e=0 (см. [5]), ныне предложены и другие классы эквивалентных проекций, близких к конформным, напр, класс: p=i, (т-n)+ke=0, k=k( и, v) - параметр класса (см. [4])..

Исследование указанных и других новых классов картографич. проекций и поиски в них наивыгоднейших проекций минимаксного типа привели к постановке задач на условный минимакс (см. [16]). Сущность таких задач заключается в том, что для данной системы дифференциальных уравнений с частными производными, решения к-рой должны быть найдены в заданной области А, требуется установить те дополнительные условия (краевые, начальные и т. д.) и в нек-рых случаях еще определить вид тех кривых, к к-рым должны быть отнесены эти условия, чтобы при интегрировании системы с ними одно из ее решений в области D наименее уклонялось бы от нуля. Известны только частные случаи исследования таких задач, основанные на методе априорных оценок решений дифференциальных уравнений. Достигнутые результаты для систем эллиптпч. типа - распространение теоремы Чебышева - Граве на два новых класса проекций: класс, описываемый системой уравнений в характеристиках п=кт,e=0, k = const>0 (см. [17]), и класс т=п ^с,e=0, с=const>0 (см. [19]). Для гиперболич. системы, описывающей эйлеровы проекции, методом характеристик установлены такие начальные условия на меридиане (см. [16]) и на параллели (см. [18]), при к-рых одно из решений системы (логарифм масштаба) в области влияния начальных данных наименее уклоняется от нуля. Картографический смысл этого аналога теоремы Чебышева таков: "носительница" данных Коши должна быть линией конформности, т. е. масштаб на ней равен единице. Этот результат при задании начальных условий на меридиане справедлив и для более широкого класса проекций: т=п ^с,e=0, c=const (см. [19]). Исследован случай эйлеровых проекций для заданной сферич. трапеции, в к-ром при рассмотрении - с привлечением интеграла энергии - смешанной задачи установлены начальные (для южной стороны трапеции) и краевые (на дугах, ограничивающих ее меридианов) условия, обеспечивающие получение для этой области наилучших эйлеровых проекций вариационного типа: на указанных трех сторонах области масштаб должен быть равен единице (см. [20]). Общая методика изыскания наивыгоднейших проекций вариационного типа для произвольной области сводится к решению вариационных задач со свободными краями (см. [4]).

Лит.:[1] Итоги науки и техники. Картография, т. 7, М., 1976, с. 45-57; [2] Каврайский В. В., Избр. труды, т. 2, в. 1-3, М., 1958-1960; [3] Каган В. Ф., Основы теории поверхностей ..., ч. 1-2, М.- Л., 1947-48; [4] Мещеряков Г. А., Теоретические основы математической картографии, М., 1968; [5] Эйлер Л., Избр. картографические статьи, пер. с нем., М., 1959; [6] Гаусс К. Ф., Избр. геодезические соч., т. 2, М., 1958; [7] Тиссо М. А., Изображение одной поверхности на другой и составление географических карт, пер. с франц., М., 1899; [8] Чебышев П. Л., Соч., т. 1, СПБ, 1899; [9] Граве Д. А., Об основных задачах математической теории построения географических карт, СПБ, 1896; [10] Марков А. А., "Изв. АН", сер. 5, 1895, т. 2, № 3, с. 177-87; [11] Урмаев Н. А., Методы изыскания новых картографических проекций, М., 1947; [12] Лаврентьев М. А., Вариационный метод в краевых задачах для систем уравнений эллиптического типа, М., 1962; [13] Мilnor J., "Атег. Math. Monthly", 1969, v. 76, p. 1101-12; [14] Airy G. В., "Philos. Mag-.", 1861, Ser. 4, v. 22, p. 409-21; [15] Цингер Н. Я., "Изв. АН", 1916, сер. 6, т. 10, № 17, с. 1693-1704; [16] Мещеряков Г. А., "Докл. АН СССР", 1961, т. 136, .N1 5, с. 1026-29; [17] Топчи лов М. А., "Изв. ВУЗов. Геод. и аэрофотосъемка", 1970, №4, с. 91-96; [18] Тучин Я. И., "Тр. Новосиб. ин-та инженеров геод., аэрофотосъемки и картографии", 1973, т. 30, с. 65-67; [19] Юзефович Ю. М., "Сб. научн. трудов Белорусок, сельхоз. академии", 1972, т. 86, с. 245-53; [20] Тучин Я. И., "Тр. Новосиб. ин-та инженеров, геод., аэрофотосъемки и картографии", 1975, т. 34, с. 55-64.

Г. А. Мещеряков.