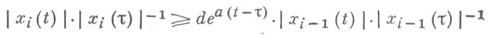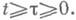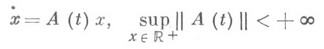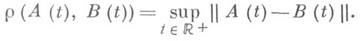ИНТЕГРАЛЬНОЙ РАЗДЕЛЕННОСТИ УСЛОВИЕ
- ИНТЕГРАЛЬНОЙ РАЗДЕЛЕННОСТИ УСЛОВИЕ
- условие на линейную систему дифференциальных уравнений 
(где A(t)- непрерывноеотображение R+
Hom(Rn, Rn), причем 
), состоящее в следующем: система имеет решения xi(t), i=1, 2,..., n, удовлетворяющие при нек-рых а>0, d>0 неравенствам
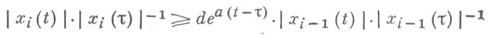
для всех i=2,..., nи всех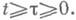 
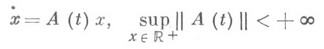
Множество систем, удовлетворяющих И. р. у., является внутренностью множества точек непрерывности всех Ляпунова характеристических показателей в пространстве систем с метрикой
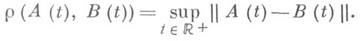
Лит.:[1] Изобов Н. А., в кн.: Итоги науки и техники. Математический анализ, т. 12, М., 1974, с. 71-146.
В. М. Миллионщиков.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "ИНТЕГРАЛЬНОЙ РАЗДЕЛЕННОСТИ УСЛОВИЕ" в других словарях:
ЛИНЕЙНАЯ СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОЧТИ ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ — система дифференциальных уравнений где почти периодические отображения; в координатной записи: тде почти периодич. числовые функции. Такие системы возникли в связи с появлением Бора почти периодических функций (см. [1]). Интерес к более узкому… … Математическая энциклопедия
УСТОЙЧИВОСТИ ТЕОРИЯ — совокупность взгля дов, представлений, идей, понятий, рассуждении, методов, теорий (содержащих определения, леммы, теоремы и доказательства), возникших и возникающих с целью изучения устойчивости движения (понимаемого в самом общем виде). Таким… … Математическая энциклопедия
УСТОЙЧИВОСТЬ ХАРАКТЕРИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ — свойство Ляпунова характеристических показателей линейной системы обыкновенных дифференциальных уравнений где непрерывное отображение (или удовлетворяющее условию Говорят, что характеристич. показатели Ляпунова системы (1) устойчивы, если каждая… … Математическая энциклопедия
