ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ТИПА СВЕРТКИ

- интегральное уравнение, содержащее искомую функцию под знаком интегрального преобразования свертки (см. Интегральный оператор). Особенностью И. у. т. с. является то, что ядра таких уравнений зависят от разности аргументов. Простейший пример - уравнение

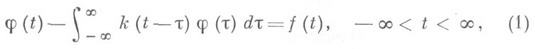
где k и f- заданные функции, а j - искомая функция. Пусть k: и 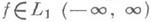и решение ищется в том же классе. Для разрешимости уравнения (1) необходимо и достаточно выполнение условия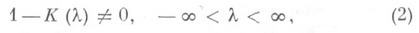

где К - преобразование Фурье функции k. При выполнении условия (2) уравнение (1) в классе L₁ имеет единственное решение, представимое формулой

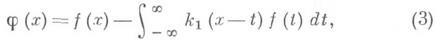
где 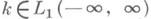однозначно определяется с помощью своего преобразования Фурье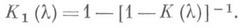

Уравнения типа свертки на полупрямой ( Винера- Хопфа уравнение)

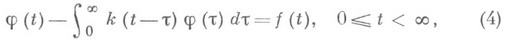
возникает при исследовании различных вопросов как теоретического, так и прикладного характера (см. [1], [4]).

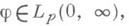
Пусть правая часть f и искомая функция 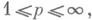а ядро и

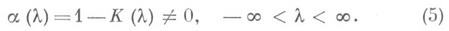
Функцию a(l)наз. символом уравнения (4). Индексом уравнения (4) называется число

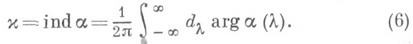
Если х= 0,функции К ₊, К _-, определенные из равенств:

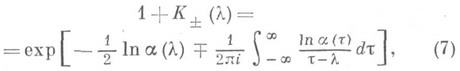
являются преобразовалиями Фурье, соответственно, функций 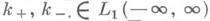таких, что k₊(t) = k_-(-t) = 0 при t<0. При указанных выше условиях уравнение (4) имеет единственное решение, которое представляется формулой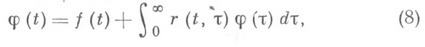

где

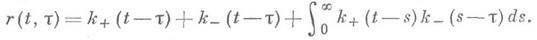
Если x<0, то все решения уравнения (4) даются формулой

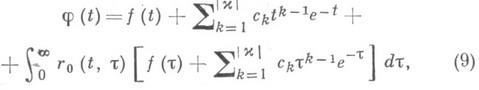
где с _k - произвольные постоянные,

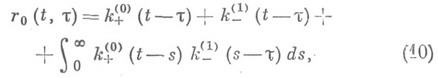
а функции 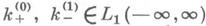однозначно определяются с помощью своих преобразований Фурье: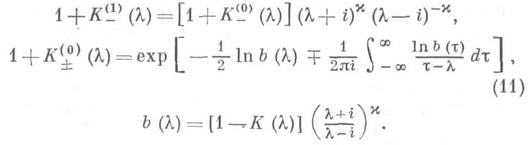

Однородное уравнение, соответствующее (4), имеет при х<0 ровно |х| линейно независимых решений j₁,..., j_|x|, являющихся абсолютно непрерывными функциями на любом конечном интервале, причем эти решения можно подобрать так, что j_k+1(t) = j'_k(t), j_k(0) = 0 при k=1,..., |х| - 1 и

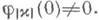
Если х>0, то уравнение разрешимо лишь при соблюдении условий:

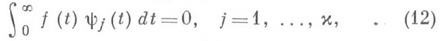
где y₁, ..., y_x- система линейно независимых решений транспонированного к (4) однородного уравнения

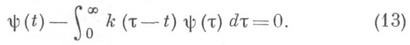
При соблюдении этих условий решение (единственное) дается формулой

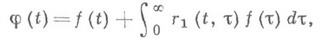
где

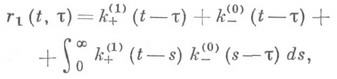
а преобразование Фурье K_-⁽⁰⁾ (X)и 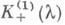функци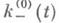й и 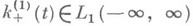определяется равенством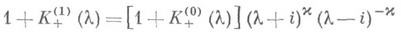

и равенствами (11). Для уравнения (4) справедливы теоремы Нётера (см. Сингулярное интегральное уравнение).

Первые значительные результаты по теории уравнений (4) были получены в [11], где указан эффективный метод (так наз. метод Винера - Хопфа) решения однородного уравнения, соответствующего (4), в предположении, что ядро и искомое решение удовлетворяют условиям: при некоторых 0<a<а и

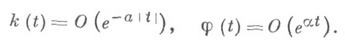
Основным моментом в методе Винера-Хопфа является идея факторизации функции h(X), голоморфной в полосе |Iml|<а, то есть идея о возможности ее представления в виде произведения h-(k)h+(k), где h_-, h₊- некоторые голоморфные функции соответственно в полуплоскостях Iml,<а и Iml>-a, удовлетворяющие нек-рым дополнительным требованиям. Эти результаты были развиты и дополнены (см. [4]).

Разработан метод сведения уравнения (4) к граничной задаче линейного сопряжения. Этим путем уравнение (4) было решено в следующих предположениях: k ОL_{1, 2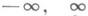} (), KОLip_a(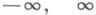), 0<a<1; К(l)=О(|l|^-b), b>0, при |l| стремистся к беск. и 1-K(l)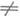0, <l<

Кроме того, была выяснена роль числа ind[1- К(k)]в решении уравнения (4). В предшествующих работах аналогичную роль играло число нулей аналитич. функции 1-К(l)в некоторой полосе (см. [3]).

Условие (5) является не только достаточным, но и необходимым для того, чтобы в случае уравнения (4) были справедливы теоремы Нётера. Приведенные решения уравнения (4) упрощаются в ряде практически важных частных случаев. Установлена асимптотика решения для специальных правых частей (см. [4]).

Уравнение (4) изучено и в случае, когда 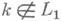(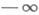, 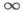) и преобразование Фурье К(l). ядра (t)имеет разрывы 1-го рода (см. [5]) или же является почти периодической функцией (см. [2]). В этих случаях условие (5) оказывается недостаточным для того, чтобы были справедливы теоремы Нётера.

Справедливость большинства перечисленных выше результатов установлена также для систем уравнений типа (4), но, в отличие от одного уравнения, системы И. у. т. с. в общем случае не решаются явно в квадратурах (см. [6]).

К И. у. т. с. относятся также парные уравнения (или дуальные уравнения)

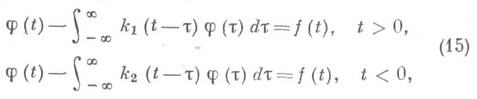
и транспонированное к ним так наз. И. у. т. с. с двумя ядрами:

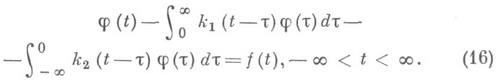
Уравнения (15) решены явно в квадратурах в [3], а уравнение (16) - в [10]. И. у. т. с. на конечном промежутке

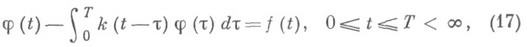
где является Фредголъма уравнением (см. [7], [9]).

И. у. т. с, символ к-рых обращается в нуль в конечном числе точек и порядки нулей - целые числа, поддаются явному решению в квадратурах (см. [8], [12]).

Лит.:[1] Нобл Б., Применение метода Винера - Хопфа, пер. с англ., М., 1962; [2] Гохберг И. Ц., Фельдман И. А., Уравнения в свертках и проекционные методы их решения, М., 1971; [3] Рапопорт И. М., "Докл. АН СССР", 1948, т. 59, № 8, с. 1403-06; "Сб. тр. ин-та матем. АН УССР", 1949, № 12, с. 102-17; [4] Крейн М. Г., "Успехи матем. наук", 1958, т. 13, в. 5, с. 3-120; [5] Дудучава Р. В., "Math. Nachr.", 1975, Bd 65, № 1, S. 59-82; [6] Гохберг И. Ц., Крейн М. Г., "Успехи матем. наук", 1957, т. 12, в. 2, с. 44-118; [7] Ганин М. П., "Изв. ВУЗов. Математика", 1963, № 2, с. 31-43; [8] Гахов Ф. Д., Смагина В. И., "Изв. АН СССР. Сер. матем.", 1962, т. 26, №. 3, с. 361-90; [9]Симоненко И. Б., "Изв. ВУЗов. Математика", 1959, №2, с. 213-26; [10] Черский Ю. И., "Уч. зап. Казанск. ун-та", 1953, т. 113, кн. 10, с. 43-56; [11] Wiеner N., Н о р f E., "Sitz. Akad. Wiss. Berlin", 1931, S. 696- 706; [12] Prossdorf S., Einige Klassen singularer Gleichungen, В., 1974.

P. В. Дудучава, Б. В. Хведелидзе.