- ЗАВИСЯЩИЙ ОТ ПАРАМЕТРОВ ИНТЕГРАЛ
- интеграл вида
в к-ром точка х=(x1, х 2, ..., х п )пробегает пространство Rn (в случае, если эта точка пробегает только нек-рую область Dв пространстве Rn, то функцию f(x, у )можно считать равной нулю при
а точка у=(y1, у 2, ..., у т), образующая совокупность параметров у 1, у 2, ..., у т, изменяется в пределах нек-рой области Gпространства Rm.Основные вопросы теории таких интегралов - это выяснение условий непрерывности и дифференцируемости функции J(y)по параметрам у 1, у 2, ..., у m.Менее стеснительные условия непрерывности и дифференцируемости J(у)получают при понимании интеграла в смысле Лебега. Справедливы следующие утверждения.
1) Если функция f(x, у )для почти всех
непрерывна по ув области 
и если существует интегрируемая в Rn функция g(x)такая, что для каждого 
и для почти всех 
справедливо неравенство 
то интеграл J(y)является непрерывной функцией ув области G.2) Если функция f(x, t), определенная при
для почти всех 
и каждого 
имеет производную 
к-рая для почти каждого 
является непрерывной функцией tна интервале (а, 6), и если существует интегрируемая в Rn функция g(x)такая, что для каждого 
и для почти всех 
справедливо неравенство 
то из существования при нек-ром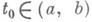 
интеграла
следует дифференцйруемость по tна интервале ( а, b )функции
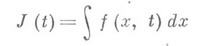
и возможность вычисления производной J'(t)дифференцированием под знаком интеграла:
Из 1)- 2) получают ряд более простых утверждений о непрерывности и дифференцируемости интегралов по параметрам, относящихся к трактовке интеграла в смысле Римана и более частным случаям (см. [2] - [4]).
Несобственные интегралы, зависящие от параметров. Для простейшего несобственного интеграла 1-го рода
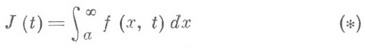
вводят понятие равномерной сходимости по параметру tна нек-ром сегменте
Этот интеграл наз. равномерно сходящимся по tна сегменте [ с, d], если для любого e>0 найдется A(e)>0 такое, что
для всех
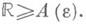
Справедливы следующие утверждения:
а)Если функция f(x, t )непрерывна в полуполосе
и интеграл (*) сходится равномерно по tна сегменте [ с, d], то функция J(t)непрерывна на сегменте 
б) Если f(x, t )и производная
непрерывны в полуполосе 
интеграл (1) сходится для нек-рого 
а интеграл
сходится равномерно относительно t на сегменте [ с, d], то функция J(t)дифференцируема на сегменте [ с, d]и ее производная может быть найдена по формуле
Аналогичные утверждения справедливы и для несобственного интеграла 2-го рода.
Лит.:[1] Владимиров В. С, Уравнения математической физики, 2 изд., М., 1971; [2] Ильин В. А., Позняк Э. Г., Основы математического анализа, ч. 2, М., 1973; [3] Кудрявцев Л. Д., Математический анализ, т. 2, М., 1970; [4] Никольский С. М., Курс математического анализа, т. 2, М., 1973; [5] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972.
В. А. Ильин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
