Гамильтонов принцип

или начало Гамильтона, в механике и математической физике служит для получения дифференциальных уравнений движения. Этот принцип распространяется на всякие материальные системы, каким бы силам они ни были подвержены; сначала мы выскажем его в том виде, какой он принимает, если силы имеют потенциал, зависящий или не зависящий от времени явным образом.

Пусть q₁, q₂, q₃ ... независимые координаты, или координатные параметры, определяющие положение материальной системы; положим, k есть число этих параметров. Пусть U есть потенциал сил, действующих на систему; U есть функция от q₁, q₂, q₃ ... и может быть еще и функцией от t. Пусть Т означает живую силу материальной системы; это есть функция от t, q₁, q₂, q₃ ... и от производных

dq₁/dt, dq₂/dt, dq₃/dt,...

относительно этих производных Т есть функция второй степени.

Если бы вопрос о движении системы при действии данных сил был решен, то координаты q выражались бы функциями времени t и 2k произвольных постоянных С₁, С₂, С₃,... ; пусть эти функции будут: f₁, f₂, f₃,...

Составим сумму T + U, которую обозначим через L. Согласно вышесказанному, это есть функция от t, координат q и их производных q'; но если мы подставим вместо q₁, q₂, q₃... соответствующие им функции f₁, f₂, f₃,..., а вместо производных q'₁, q'₂,... производные по t от соответствующих функций f, то L обратится в функцию от t и от 2k произвольных постоянных С.

Предположив, что L выражена таким образом, возьмем интеграл от Ldt между произвольными пределами: нижним t₁ и верхним t₂; полученный интеграл, который обозначим через S:

будет функцией от t₂, t₁ и величины С.

Предположим, что положения материальной системы в моменты t₁ и t₂ вполне обозначены, так что координаты q имеют определенные значения для момента t₁ и другие определенные значения для момента t₂, тогда по этим 2k данным найдется по меньшей мере одна совокупность значений 2k величин С₁, С₂, С₃,... ; обозначим найденные величины малыми с₁, с₂, с₃,....

Под влиянием данных сил материальная система перейдет из данного первого положения в положение второе по таким путям, на которых вышесказанные величины С будут сохранять постоянные значения с₁, с₂, с₃ ...; эти пути или этот путь системы условимся называть прямым путем.

Однако есть возможность перевести ту же материальную систему из первого положения во второе в течение времени (t₂-t₁) по другому, окольному, пути; для этого надо присоединить к данным силам еще новые силы или же сообщить ей во время движения ряд толчков. Так как добавочные силы или толчки могут быть бесконечно разнообразны, то и окольные пути будут столь же разнообразны. На каждом из окольных путей C будут уже не постоянны, но будут изменяемы с течением движения в зависимости от вида окольного пути; но только они должны будут иметь значения с₁, с₂, с₃,.... в конечных положениях системы — первом и втором.

Предположим, что будем рассматривать окольные пути бесконечно мало отличающиеся от прямого; тогда значения С на этих путях будут отличаться от постоянных с₁, с₂, с₃,.... на ничтожно малые величины δС₁, δС₂, δС₃, которые мы назовем вариациями этих постоянных. Вариации δС₁, δС₂, δС₃,... суть функции от t произвольного вида, обращающиеся в нуль при t₁ и t₂ и имеющие ничтожно малые величины при промежуточных значениях t.

Если постоянные С получают вариации на окольных путях, то и величина S варьируется. Принцип Гамильтона состоит в том, что вариация первого порядка интеграла S равна нулю для всяких окольных путей, бесконечно мало отличающихся от прямого.

Равенство δS=0 может быть представлено следующим образом:

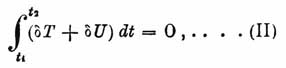причем вариации от Т и U можно представить в виде сумм:

δT = Σ(dT/dq')δq' + Σ(dT/dq)δq

δU = Σ(dU/dq)δq.

Поступив с равенством (II) так, как объяснено в статье "Вариационное исчисление" (см.), получим из равенства (II), выражающего принцип Гамильтона, Лагранжевы дифференциальные уравнения движения рассматриваемой материальной системы, т. е. уравнения:

d/dt[dL/dq₁'] = dL/dq₁

d/dt[dL/dq₂'] = dL/dq₂ и проч.

Подробнее о начале Гамильтона см. С. G. J. Jacobi, "Vorlesungen über Dynamik" (1866), или в полном издании сочинений Якоби, Supplementband.

Равенство δS = 0 выражает, что интеграл S есть minimum, maximum или minimax; для суждения о том, который из этих случаев имеет место, надо составить и определить знак вариации второго порядка от S.

Принцип Гамильтона имеет место и тогда, когда силы не имеют потенциала; он тогда выражается так:

где Q есть составляющая сил по координатному параметру q. О применении этого принципа к составлению дифференциальных уравнений гидродинамики и теории упругости см. Kirchhoff, "Vorlesungen über mathematische Physik", "Mechanik" (1874); "Mathematical papers of the late George Green" (1871).

Д. Б.