ДРОБНАЯ СТЕПЕНЬ

линейного оператора Ав комплексном банаховом пространстве Е- функция f{A )от этого оператора такая, что f(z)=z^a. Если оператор Аограничен, и спектр его не содержит и не окружает нуля, то А ^a определяется Коши интегралом по контуру, окружающему спектр A и не содержащему внутри себя нуль. Если Анеограничен, то контур приходится брать бесконечным, и возникают вопросы об условиях сходимости интеграла. Если Аимеет плотную в Еобласть определения D(А)и при l<0 имеет резольвенту с оценкой

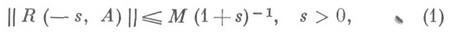
то

где Г состоит из сторон угла, строящегося по М. Операторы А ^-a ограничены и при любом и Положительные степени определяются так: А ^a =( А ^-a)^-1;они уже являются неограниченными. При любых действительных a и b выполнено основное свойство степеней

для и g=mах{a, b, a+b}. При 0<a<1 (А ^a)^b=А^ab. При любых a<b<g и

(неравенство моментов). Полугруппа степеней А ^-a допускает расширение до полугруппы A^-z, аналитической в правой полуплоскости.

Ряд приведенных свойств Д. с. обобщается на случай, когда Ане имеет ограниченного обратного и справедлива оценка s>0. При условии (1) и при 0<а<1

Если оператор В- производящий оператор сжимающей полугруппы U(t), то

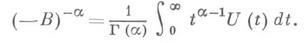
Из условия (1) не вытекает, что -А является производящим оператором сильно непрерывной полугруппы, но оператор - А ^a. при является производящим оператором аналитич. олугруппы.

Оператор Вподчинен оператору А, если и Если Вподчинен Аи резольвенты обоих операторов обладают свойством (1), то В ^a. подчинен А ^b. при

Если А- положительный самосопряженный оператор в гильбертовом пространстве, то его Д. с. определяется через спектральное разложение

В неравенстве моментов для такого оператора константа с(a, b, g)=1. Пусть Аи В- два самосопряженных положительных оператора, действующие в гильбертовых пространствах Ни Н ₁ соответственно. Если Т- такой ограниченный линейный оператор из Нв Н ₁ с нормой М, что и

то и

(неравенство Хайнца). В частности, при H=H₁ и Т=I из подчиненности Воператору Аследует подчиненность В ^a оператору А ^a при Д. с. операторов применяются при исследовании нелинейных уравнений. Они детально изучены для операторов, порожденных эллиптич. праевыми задачами.

Лит.:[1] Функциональный анализ. [Справочная математическая библиотека], 2 изд., М., 1972; [2] Крейн С. Г., Линейные дифференциальные уравнения в банаховом пространстве, М., 1967; [3] Сили Р., "Математика", 1988, т. 12, № 1, с. 96 - 112.

С. Г. Крейн.