ГОЛОМОРФНОСТИ ОБЛАСТЬ

ГОЛОМОРФНОСТИ ОБЛАСТЬ

область Dкомплексного пространства , для к-рой существует функция f(z), голоморфная в Dи не продолжаемая голоморфно в большую область; при этом Dназ. естественной областью определения функции f(z). Напр., естественной областью определения функции


служит единичный круг, к-рый поэтому является Г. о.

в . В всякая область есть Г. о. Напротив, в , , не всякая область есть Г. о. Так, никакая область вида , где К- компакт, содержащийся в D, не будет Г. о.

Область наз. голоморфно выпуклой, если для каждого множества существует такое содержащее Амножество , что для любой точки существует функция , голоморфная в Dи такая, что


Для того чтобы область Dбыла Г. о., необходимо и достаточно, чтобы она была голоморфно выпуклой (теорема Картана - Туллена). Для того чтобы область Dбыла Г. о., необходимо и достаточно, чтобы для каждой точки существовал барьер - функция 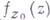, голоморфная в D и не продолжимая голоморфно в точку 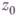. Напр., если D- произвольная область в , то функция есть барьер в любой точке 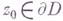, так что Dесть Г. о.; если D - выпуклая область в С n и


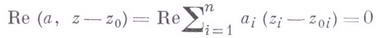
- опорная плоскость в точке 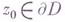, то функция есть барьер в 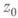, и поэтому всякая выпуклая область в есть Г. о.

Пересечение Г. о. есть Г. о.; всякое биголоморфное отображение переводит Г. о. в Г. р.; сумма возрастающей последовательности Г. о. есть Г. о. (теорема Бенке- Штейна).

Область наз. псевдовыпуклой, если функция-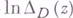 есть плюрисубгармоническая. функция в D, где 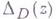есть расстояние от точки 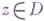до Для того чтобы область была Г. о., необходимо и достаточно, чтобы она была псевдовыпуклой (теорема Ока). Достаточность условия в теореме Ока составляет содержание проблемы Леви, поставленной Э. Леви (Е. Levi, в 1911). Для она была решена К. Ока (К. Ока, 1942); для эта проблема решена независимо К. Ока, Ф. Норгэ, Г. Бремерманом (F. Norguet, H. Bremermann, 1953-1954).

Г. о. с достаточно гладкой границей допускают локальное описание. Область наз. псевдовыпуклой в точке 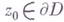, если существует такая окрестность Vточки 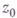и такая определенная в Vдей-ствительна-я функция 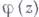класса , что: а)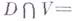 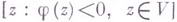и б) на плоскости


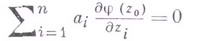
форма Гессе


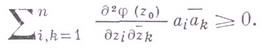
Если в условии б) имеет место строгое неравенство для всех рассматриваемых векторов , то область Dназ. строго псевдовыпуклой в точке гД. Область Dназ. (строго) псевдовыпуклой всмысле Леви, если она (строго) псевдовыпукла в каждой точке .

Если область строго псевдовыпукла в смысле Леви, то она псевдовыпукла (теорема Леви).

Г. о. функции , заданной в первоначальной окрестности , может быть построена при помощи разложений в ряды Тейлора с использованием принципа голоморфного продолжения; при этом может оказаться, что в построенной области голоморфно продолженная функция 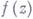неоднозначна. Чтобы сделать функцию однозначной, необходимо расширить понятие области. Это достигается путем введения римановых областей ( наложения областей, неоднолистных областей) над 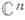(римановы области над наз. римановыми поверхностями). Понятие Г. о. распространяется и на римановы области и даже на объекты более общей структуры - комплексные многообразия и комплексные пространства. Обобщение понятия Г. о. приводит к Штейна пространствам.

Лит.:[1] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964; [2] Шабат Б. В., Введение в комплексный анализ, 2 изд., ч. 2, М., 1976; [3] Xёрмандер Л., Введение в теорию функций нескольких комплексных переменных, пер. с англ., М.. 1968.

В. С. Владимиров.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем написать курсовую

Полезное


Смотреть что такое "ГОЛОМОРФНОСТИ ОБЛАСТЬ" в других словарях:

  • ГОЛОМОРФНОСТИ ОБОЛОЧКА — (римановой) области D наибольшая область H(D), обладающая тем свойством, что всякая функция, голоморфная в D, голоморфно продолжается в Н(D). Задача построения для данной области Dее Г. о. возникает в связи с тем, что в комплексном пространстве… …   Математическая энциклопедия

  • РИМАНОВА ОБЛАСТЬ — к о м п л е к с н о е (а н ал и т и ч е с к о е) м н о г о о б р а з и е н а д , аналог римановой поверхности аналитич. функции w=f(z) одного комплексного переменного z для случая аналитич. ции w=f(z), z=(z1; . . . , zn), многих комплексных… …   Математическая энциклопедия

  • ТРУБЧАТАЯ ОБЛАСТЬ — труба, область Тв комплексном пространстве вида где В область в действительном подпространстве к рая наз. основанием Т …   Математическая энциклопедия

  • НЕПРЕРЫВНОСТИ ТЕОРЕМА — принцип непрерывности: пусть G голоморфности область в любые последовательности множеств, для к рых имеет место принцип максимума относительно модулей функции f, голоморфной в G, т. е. тогда если сходятся к нек рому ограниченному множеству S, а к …   Математическая энциклопедия

  • АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО — обобщение понятия аналитического многообразия. Локальной моделью (и одновременно важнейшим примером) аналитич. ространства над полным недискретно нормированным полем kявляется аналитическое множество в области n мерного пространства над полем k,… …   Математическая энциклопедия

  • БИГОЛОМОРФНОЕ ОТОБРАЖЕНИЕ — голоморфный изоморфизм, голоморфизм, псевдоконформное отображение, обобщение однолистного конформного отображения на случай нескольких комплексных переменных. Голоморфное отображение области на область наз. биголоморфным отображением, если оно… …   Математическая энциклопедия

  • КВАНТОВАЯ ТЕОРИЯ ПОЛЯ — теория релятивистских квантовых систем. Возникновение К. т. п. связано с задачами о взаимодействии вещества с излучением и с попытками построения релятивистской квантовой механики [П. Дирак (P.A.M. Dirac, 1927), В. Гейзенберг (W. Heisenberg), В.… …   Математическая энциклопедия

  • АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция, к рая может быть представлена степенным рядом. Исключит, важность класса А. ф. определяется следующим. Во первых, этот класс достаточно ш и р о к: он охватывает большинство функций, встречающихся в основных вопросах математики и ее… …   Математическая энциклопедия

  • ДИРИХЛЕ РЯД — функциональный ряд вида где а п комплексные коэффициенты; l п, 0< показатели Д. p., s= s+ it комплексное переменное. При ln=ln пполучается так наз. обыкновенный ряд Дирихле Ряд представляет для s>1 дзета функцию Римана. Ряды где х(п)… …   Математическая энциклопедия

  • ОСОБАЯ ТОЧКА — 1) О. т. аналитической функции f(z) препятствие для аналитического продолжения элемента функции f(z) комплексного переменного zвдоль какого либо пути на плоскости этого переменного. Пусть аналитическая функция f(z) определена некоторым… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»