ГОЛОМОРФ ГРУППЫ

- понятие теории групп, возникшее в связи с решением следующей задачи. Можно ли включить любую данную группу Gв качестве нормальной подгруппы в нек-рую другую группу так, чтобы все автоморфизмы группы Gбыли следствиями внутренних автоморфизмов этой большей группы? Для решения такой задачи строят по группе Gи ее группе автоморфизмов новую группу Г, элементами к-рой являются пары , где 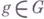, , 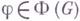и в к-рой определяется композиция пар по следующей формуле:

здесь 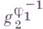- образ элемента 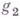при автоморфизме 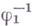Группа Г (или изоморфная ей группа) наз. голоморфом группы G. Множество пар вида (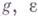), где 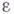- единица группы Ф(G), составляет подгруппу, изоморфную исходной группе G. Аналогично, пары вида (), где - единица группы G, составляют подгруппу, изоморфную группе Ф(G). Формула пока зывает, что группа Г в действительности является решением поставленной задачи.

В. Н. Ремесленников.